在计算机图形学中,矩阵乘法有着很好的应用。图形的变换可以通过构造相应的矩阵进行计算来完成。
我们知道,平面上的元素,就是点、线、面,而线就是由一个个点组成的,面是由一条条线组成的,所以归根结底,平面上所有的图形都是由点组成的。在坐标系中,一个点就是由一对x,y值组成的,p = {x, y}。在平面上,过两点间的,可以画一条直线,所以我们一般通过 两个点p1, p2可定义一条直线,e = {p1, p2},而图形呢,则是由众多的点和点之间的的线段组成的。所以,平面上的图形变换,本质是点坐标位置的变换。
在平面中,常用的基本图形变换有以下四种:
1)平移(Translation)。
设点(x,y)水平向右平移dx个单位,垂直向上平移dy个单位。表示点(x,y)的矩阵P和构造的平移变换矩阵T如下:

则点(x,y)的平移后的新位置P'可以通过矩阵乘法计算出来。
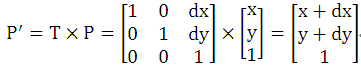
2)缩放(Scale)。
设点(x,y)在水平方向和垂直方向的缩放比例分别为Sx和Sy。表示点(x,y)的矩阵P和构造的缩放变换矩阵S如下:
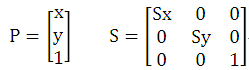
则点(x,y)的缩放后的新位置P'可以通过矩阵乘法计算出来。

3)旋转(Rotation)。
设点(x,y)绕原点逆时针旋转α角度。表示点(x,y)的矩阵P和构造的旋转变换矩阵R如下:

旋转矩阵的构造原理参见下图。

则点(x,y)绕原点逆时针旋转后的新位置P'可以通过矩阵乘法计算出来。

4)反射(Reflect)。
反射变换分为关于原点反射、关于x轴反射和关于y轴反射三种。
点 p(x,y) 关于原点反射后得到的点为po'(-x,-y)。
点 p(x,y) 关于x轴反射后得到的点为px'(x,-y),也称为上下翻转。
点 p(x,y) 关于x轴反射后得到的点为py'(-x,y),也称为左右翻转。
三种反射的矩阵计算如下:

【例1】点的变换。
描述
平面上有不超过10000个点,坐标都是已知的,现在可能对所有的点做以下几种操作:
平移一定距离(M),相对X轴上下翻转(X),相对Y轴左右翻转(Y),坐标缩小或放大一定的倍数(S),所有点对坐标原点逆时针旋转一定角度(R)。
操作的次数不超过10000次,求最终所有点的坐标。
输入
测试数据的第一行是两个整数N,M,分别表示点的个数与操作的个数(N,M<=10000)
随后的一行有N对数对,每个数对的第一个数表示一个点的x坐标,第二个数表示y坐标,这些点初始坐标大小绝对值不超过100。
随后的M行,每行代表一种操作,行首是一个字符:
首字符如果是M,则表示平移操作,该行后面将跟两个数x,y,表示把所有点按向量(x,y)平移;
首字符如果是X,则表示把所有点相对于X轴进行上下翻转;
首字符如果是Y,则表示把所有点相对于Y轴进行左右翻转;
首字符如果是S,则随后将跟一个数P,表示坐标放大P倍;
首字符如果是R,则随后将跟一个数A,表示所有点相对坐标原点逆时针旋转一定的角度A(单位是度)
输出
每行输出两个数,表示一个点的坐标(对结果四舍五入到小数点后1位,输出一位小数位)
点的输出顺序应与输入顺序保持一致
样例输入
2 5
1.0 2.0 2.0 3.0
X
Y
M 2.0 3.0
S 2.0
R 180
样例输出
-2.0 -2.0
0.0 0.0
(1)编程思路。
直接按前面的介绍内容,分别构造5类变换矩阵。定义矩阵ans初始为单位矩阵。然后每输入m种操作中的一种时,根据操作类型构造相应的变换矩阵temp,然后ans右乘temp,即ans=temp*ans。输入完m种操作后,得到的ans矩阵就是每个点的变换矩阵,进行变换矩阵与点的矩阵乘法就可以得到每个点的最终坐标。
(2)源程序。
#include <stdio.h>
#include <string.h>
#include <math.h>
#define PI acos(-1.0)
#define MAXN 10005
struct Matrix
{
double mat[4][4]; // 存储矩阵中各元素
};
struct Point
{
double x ,y ;
};
Matrix matMul(Matrix a ,Matrix b,int n)
{
Matrix c;
memset(c.mat,0,sizeof(c.mat));
int i,j,k;
for (k = 1; k<=n ; k++)
&