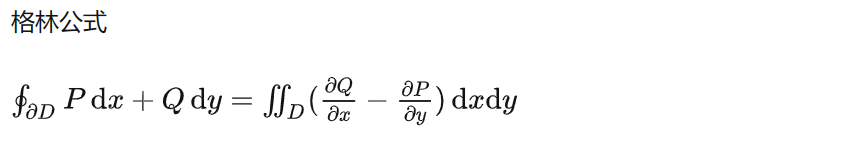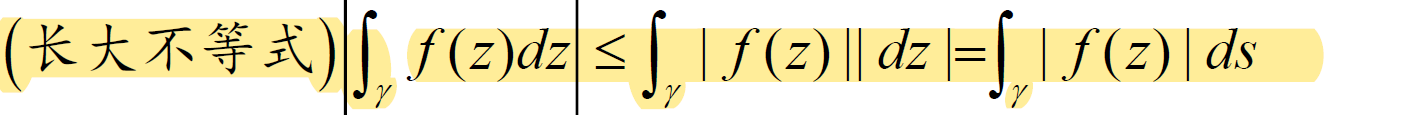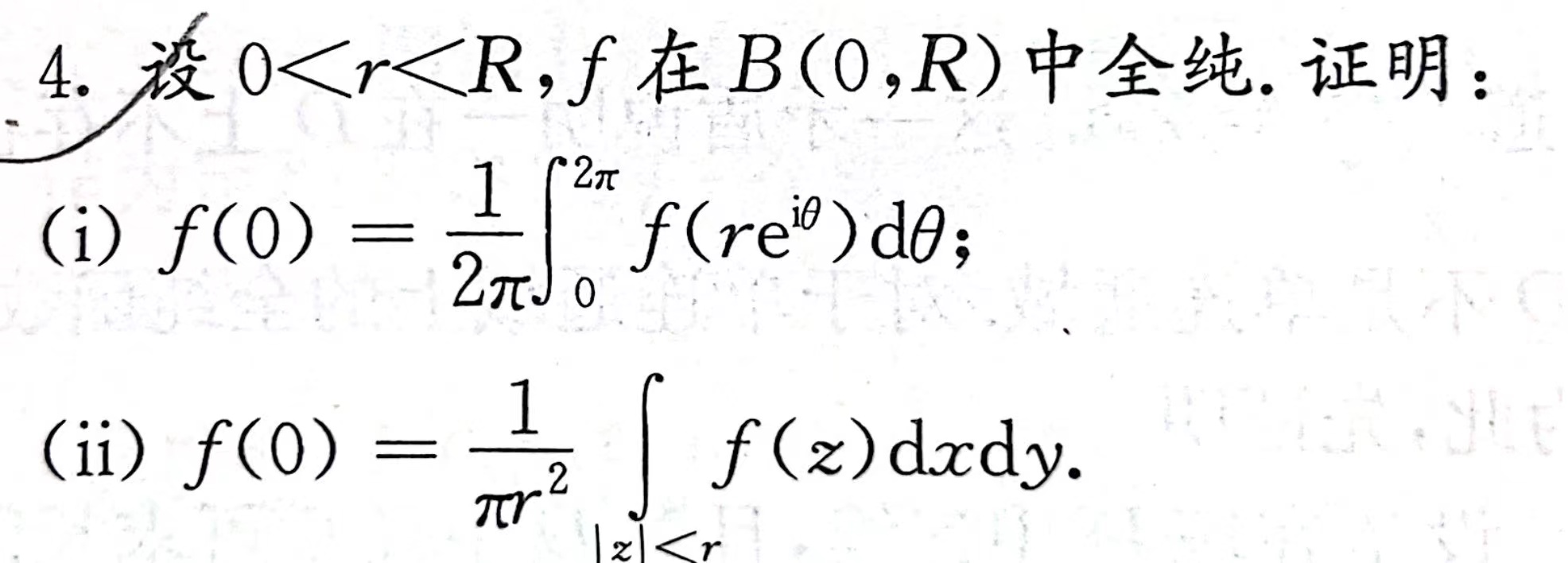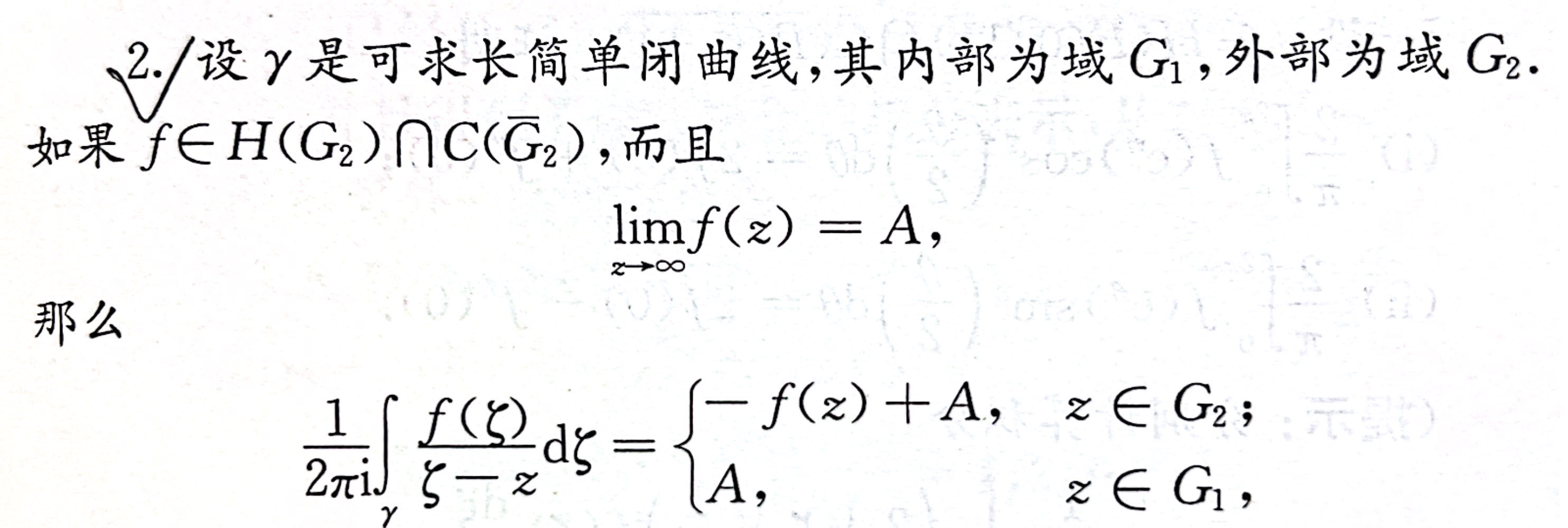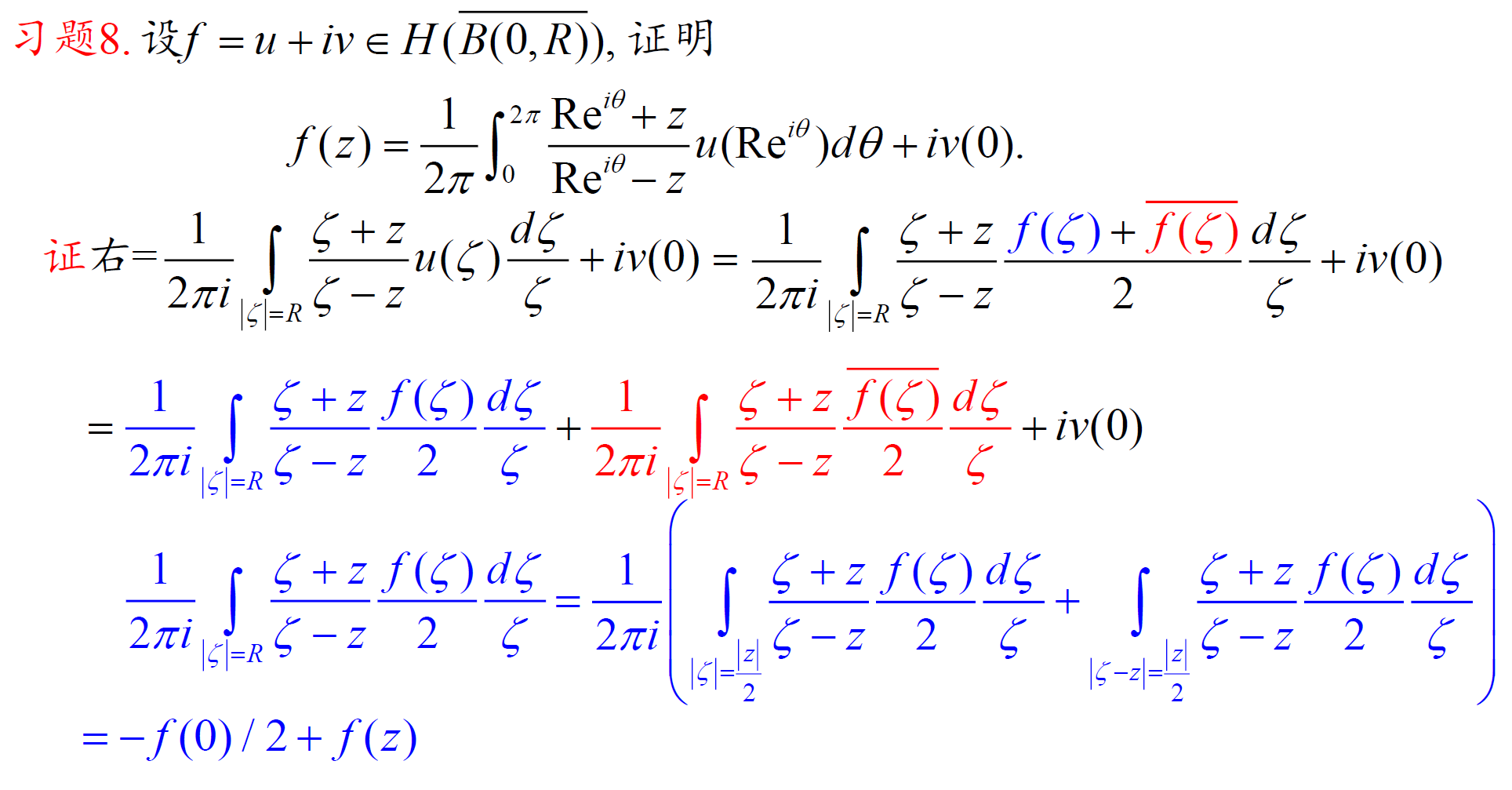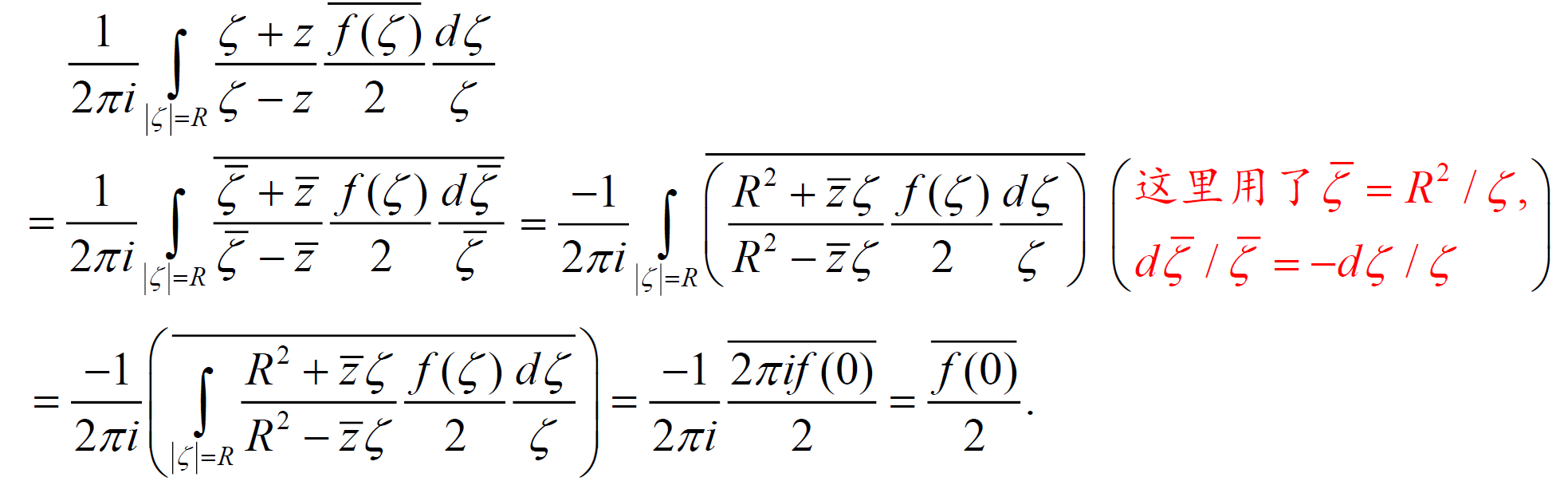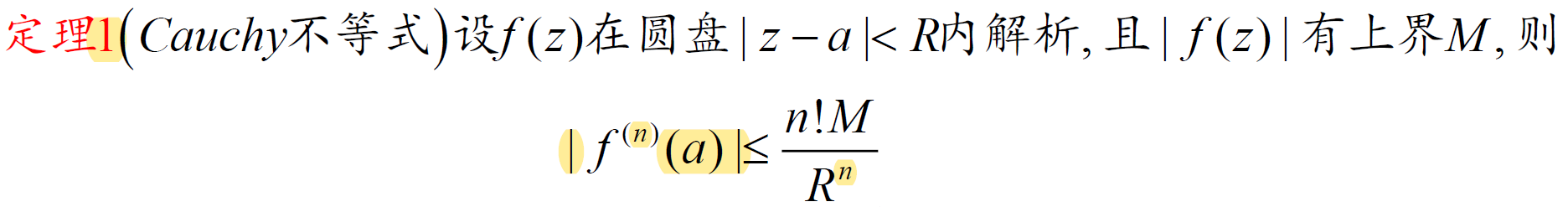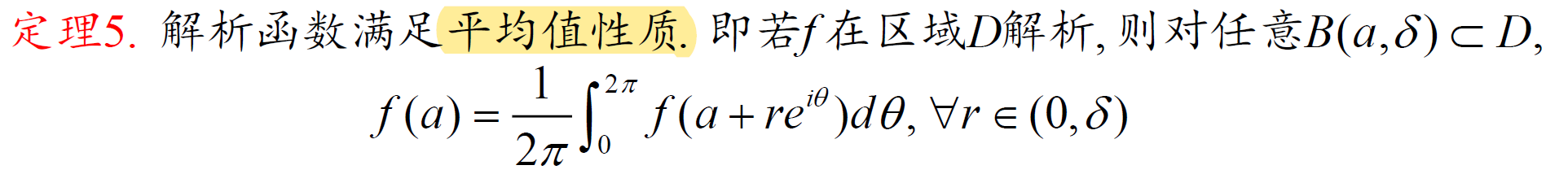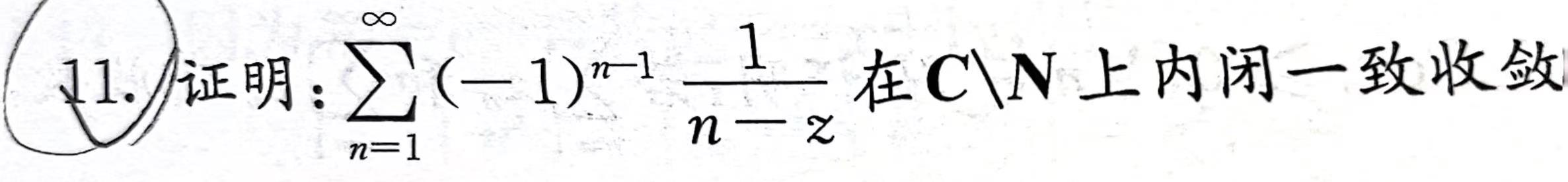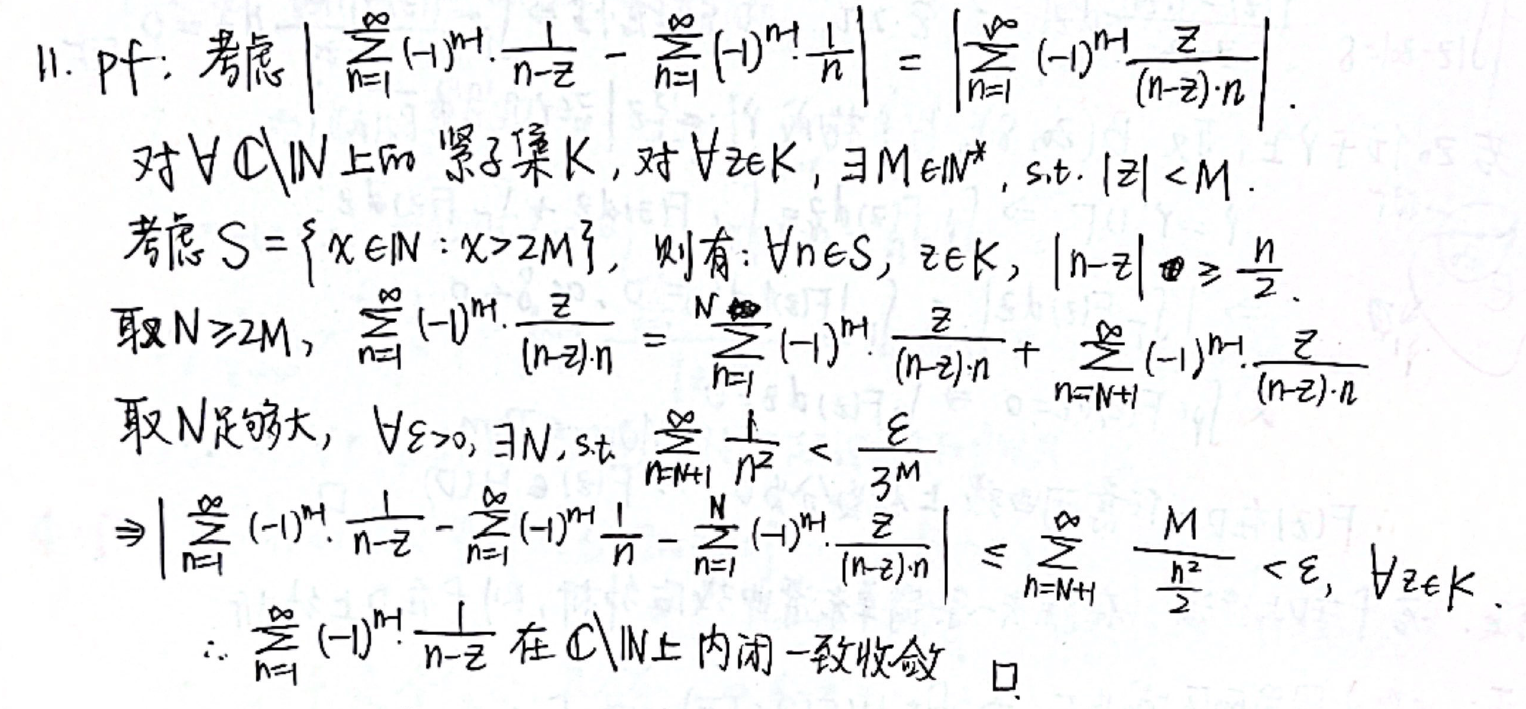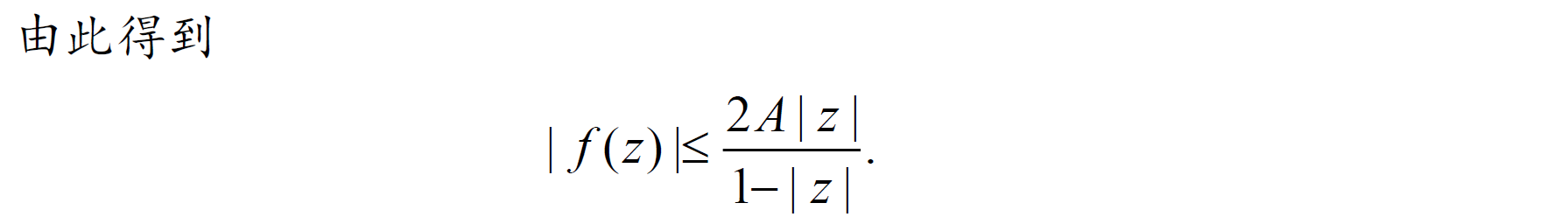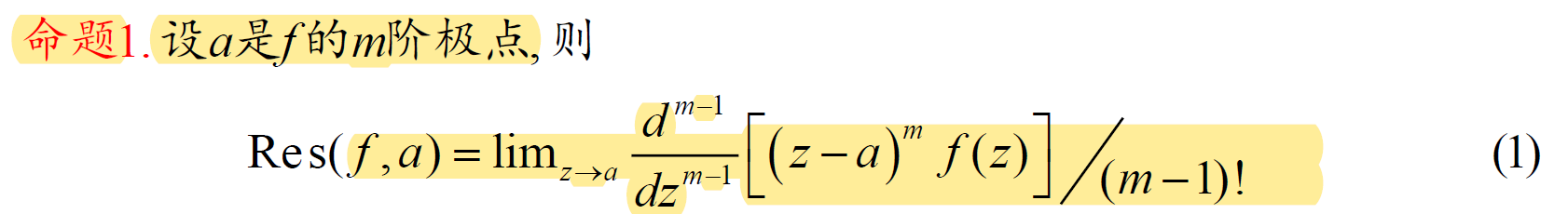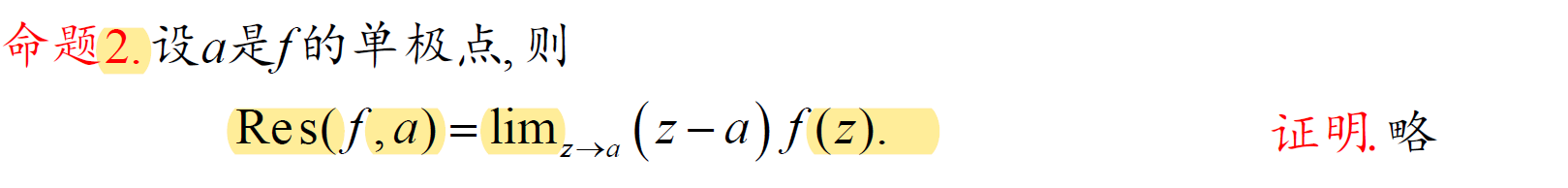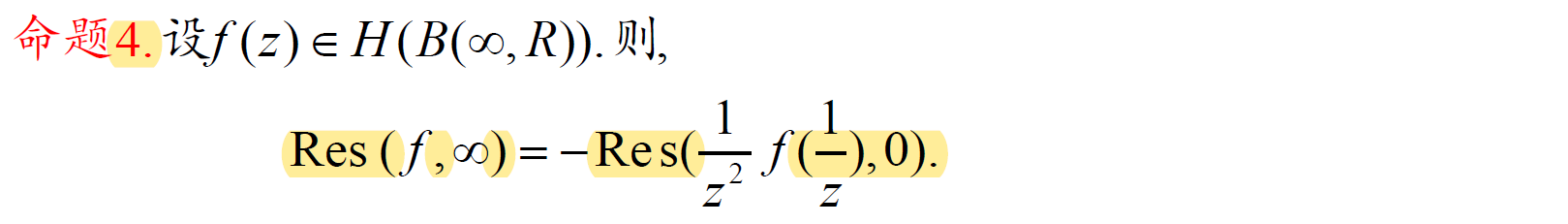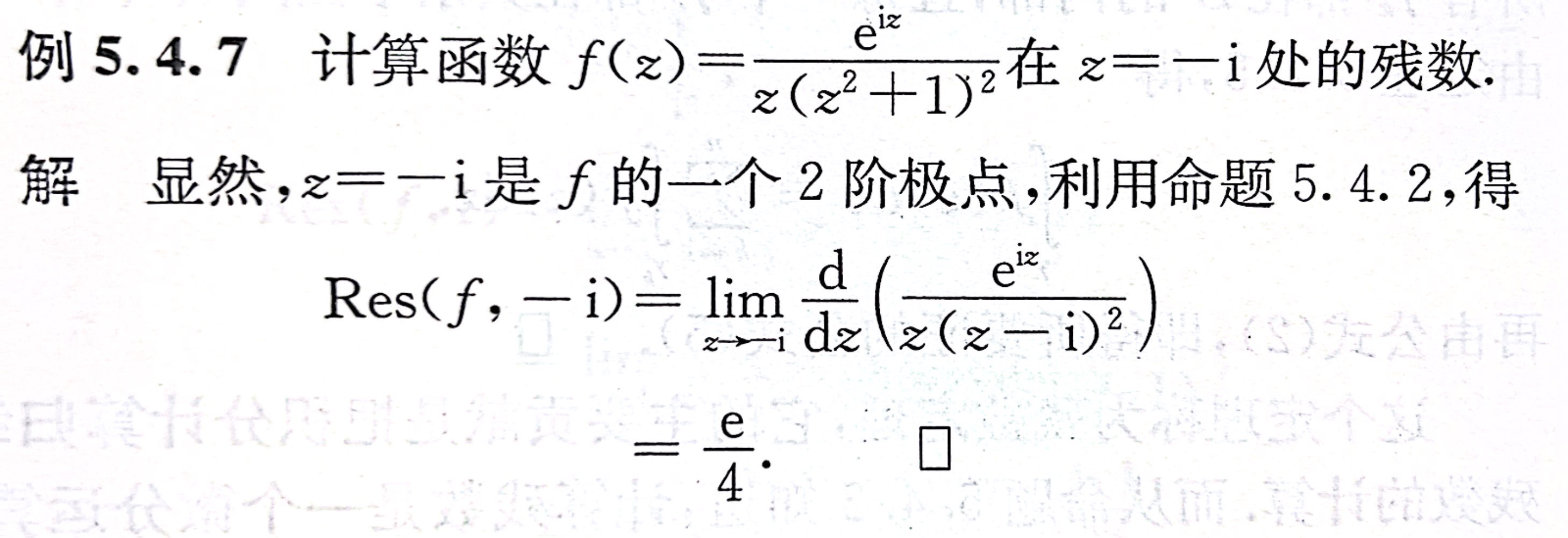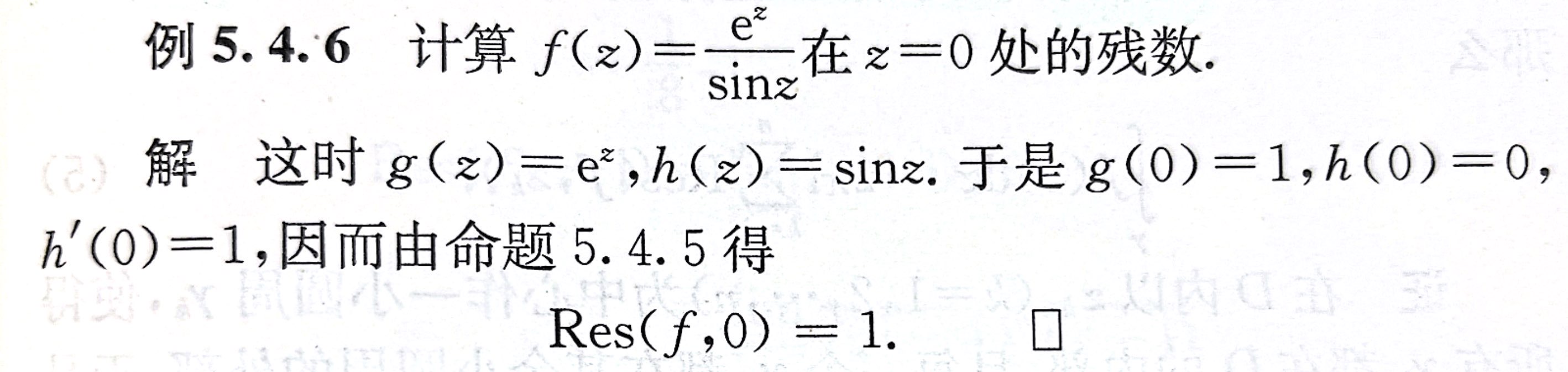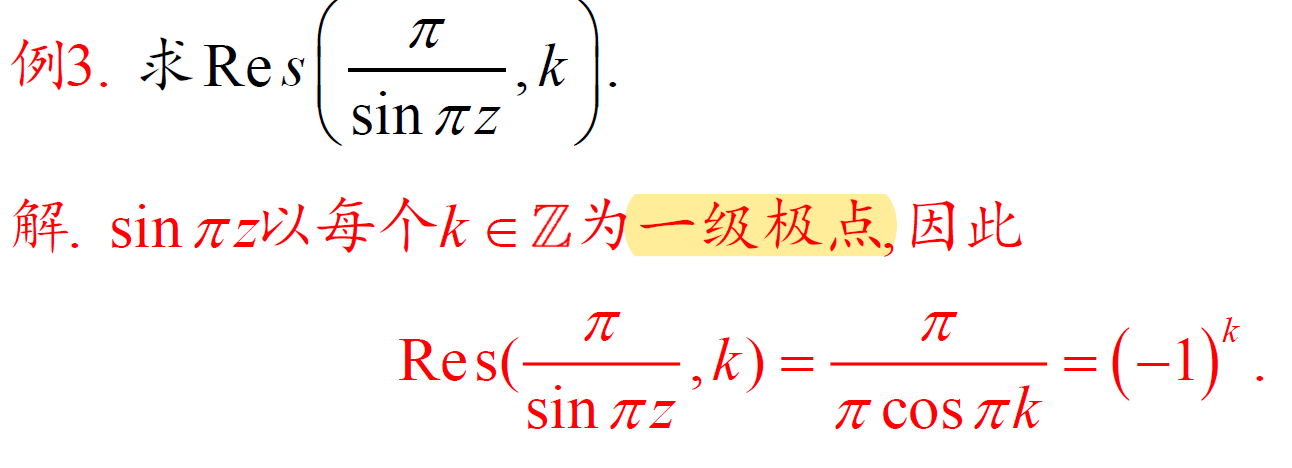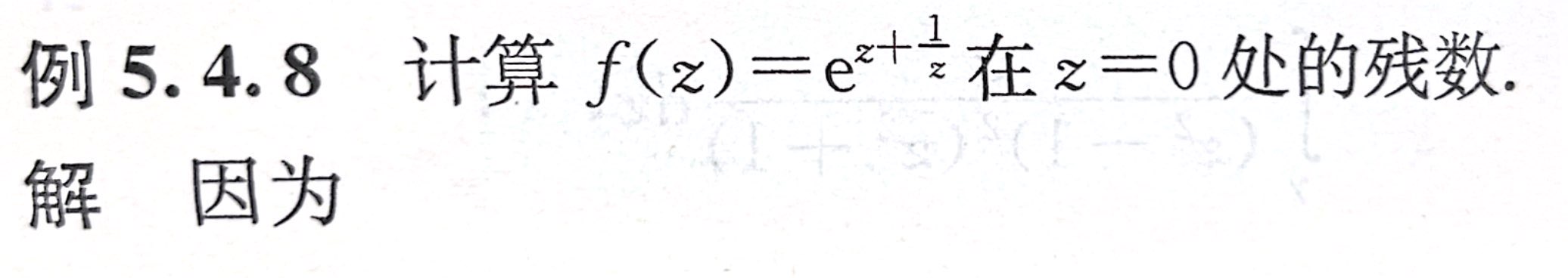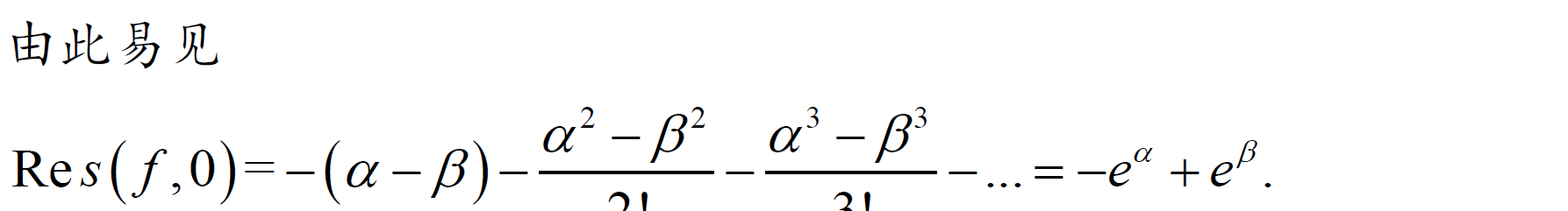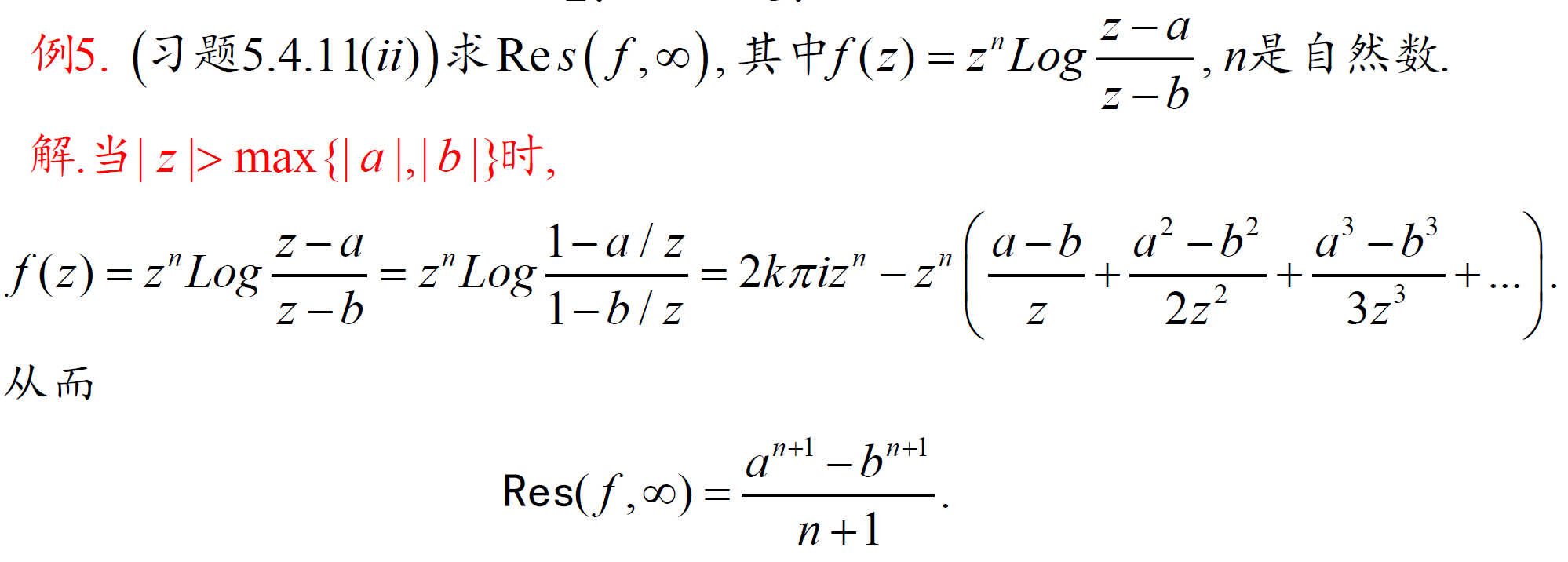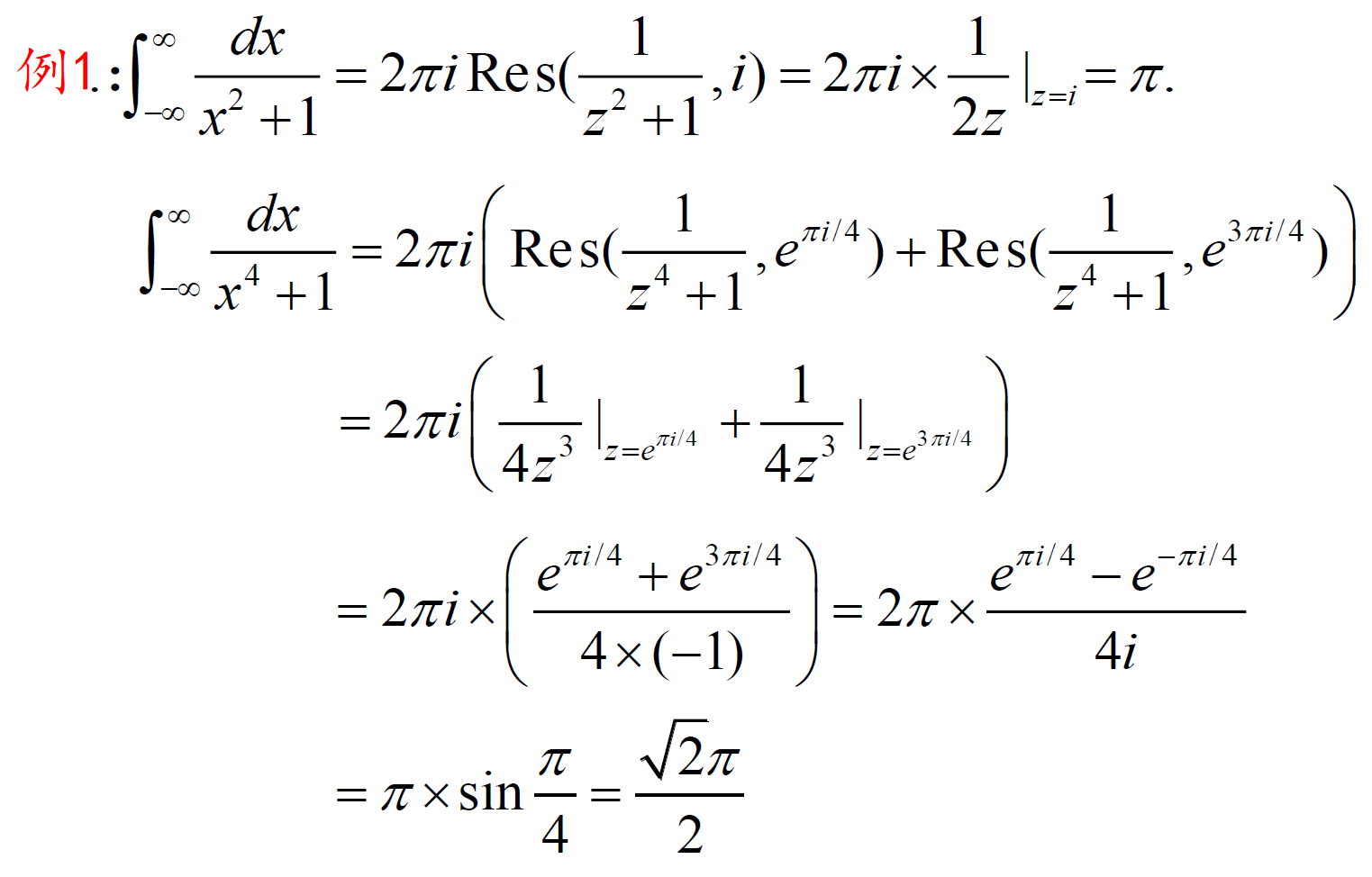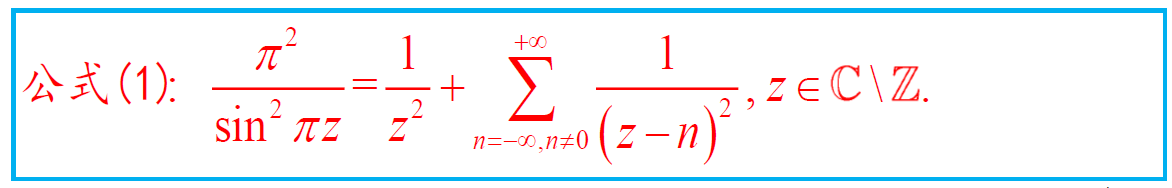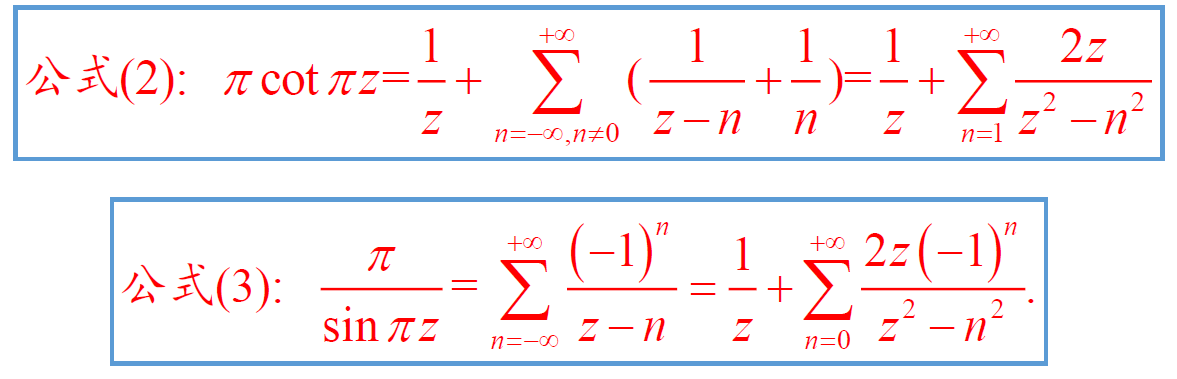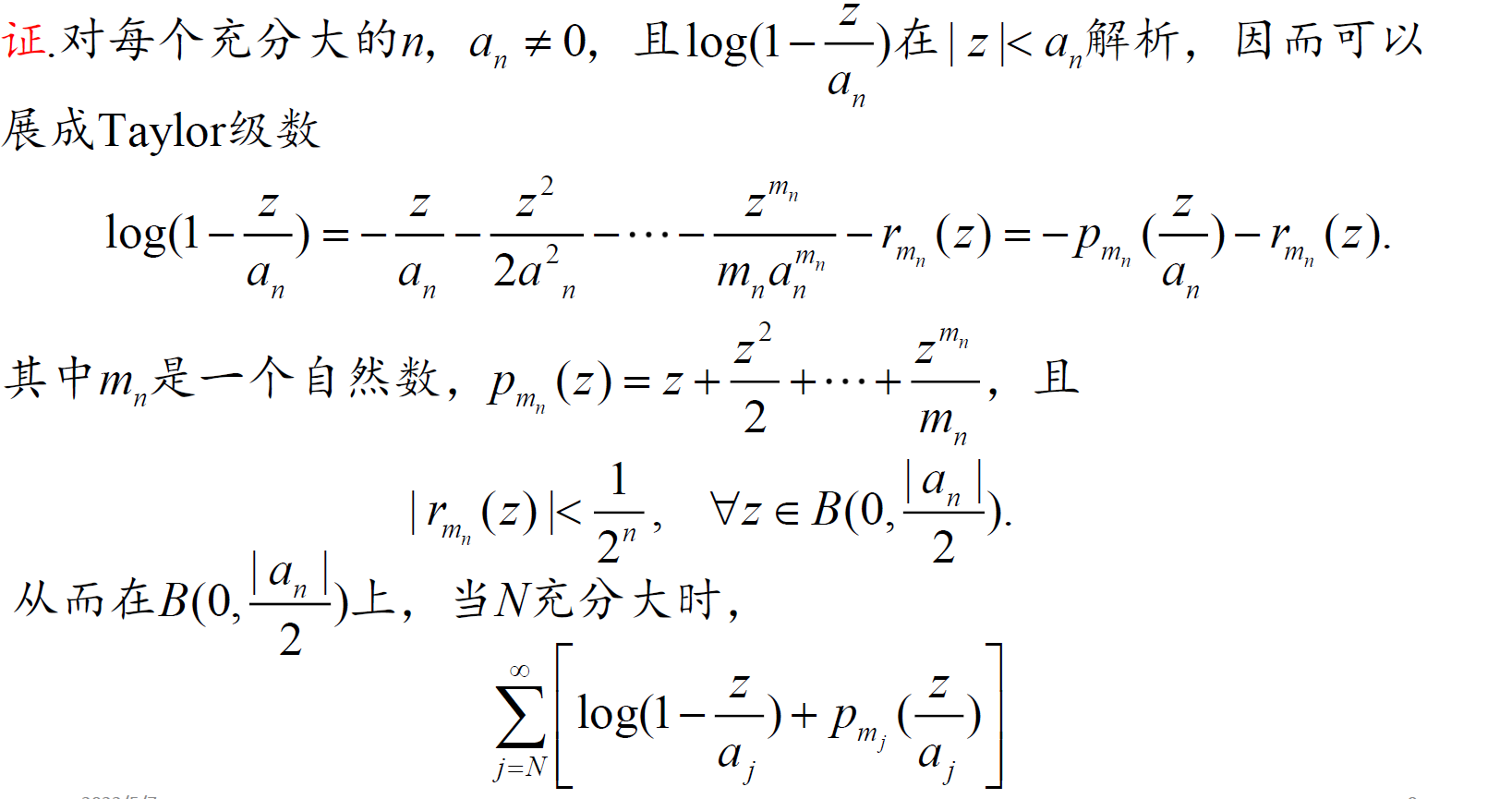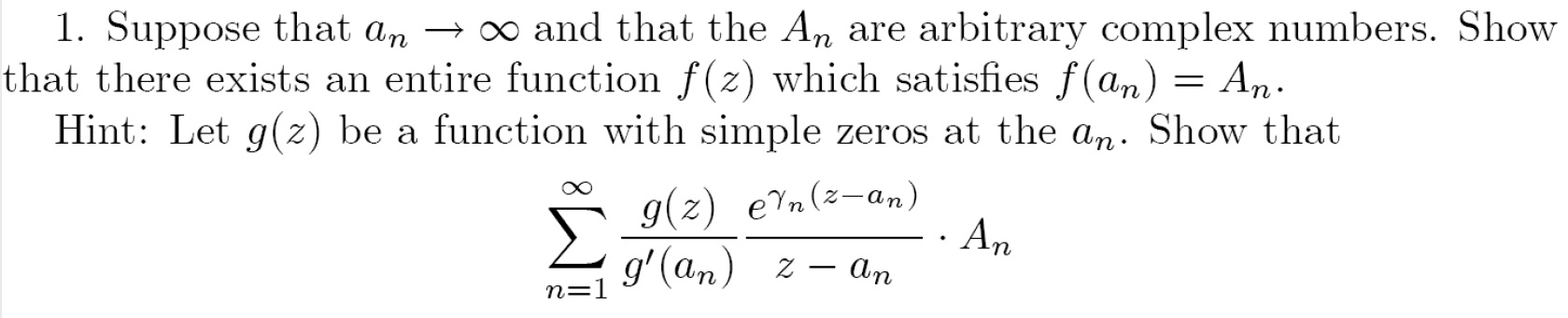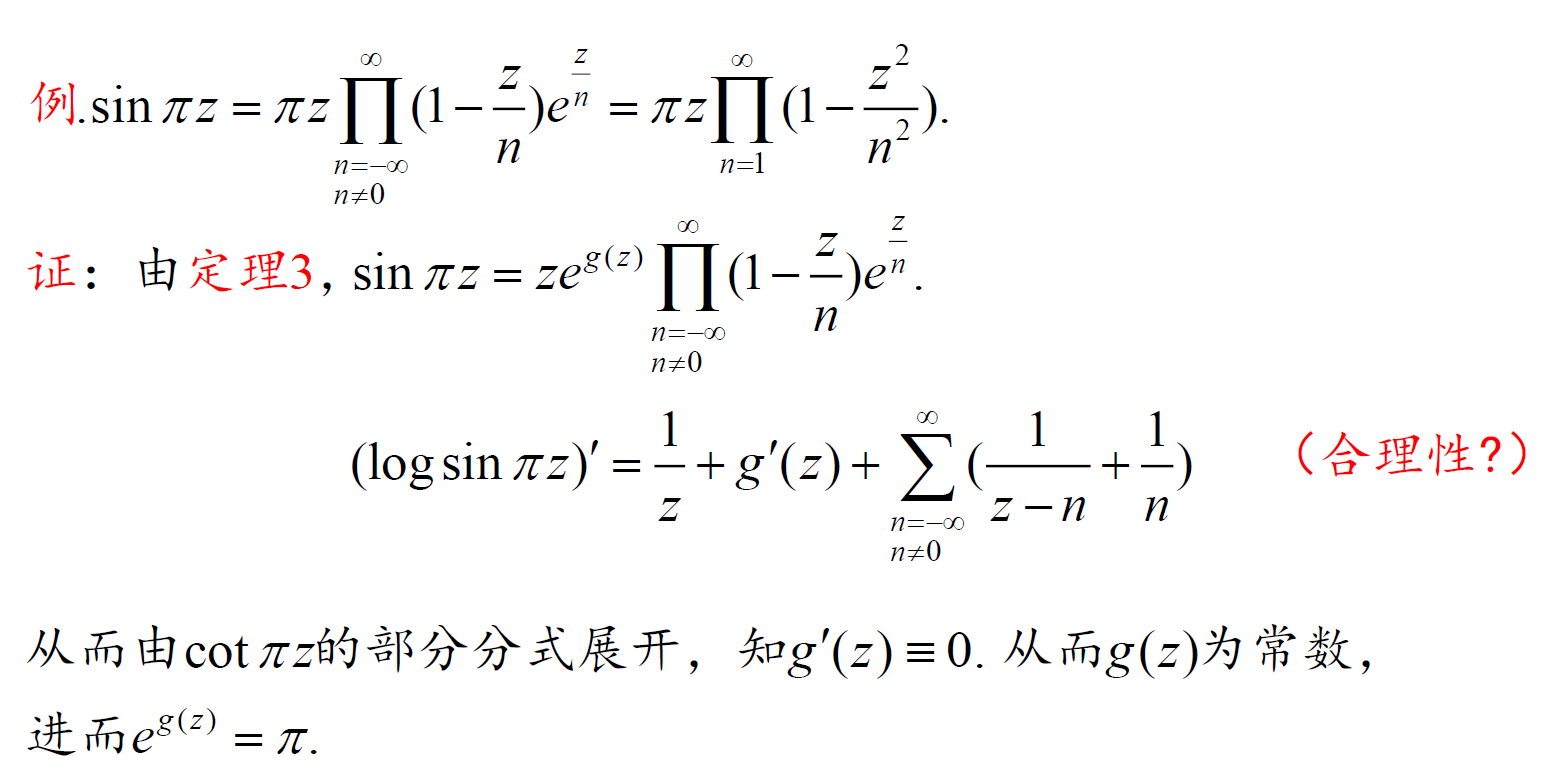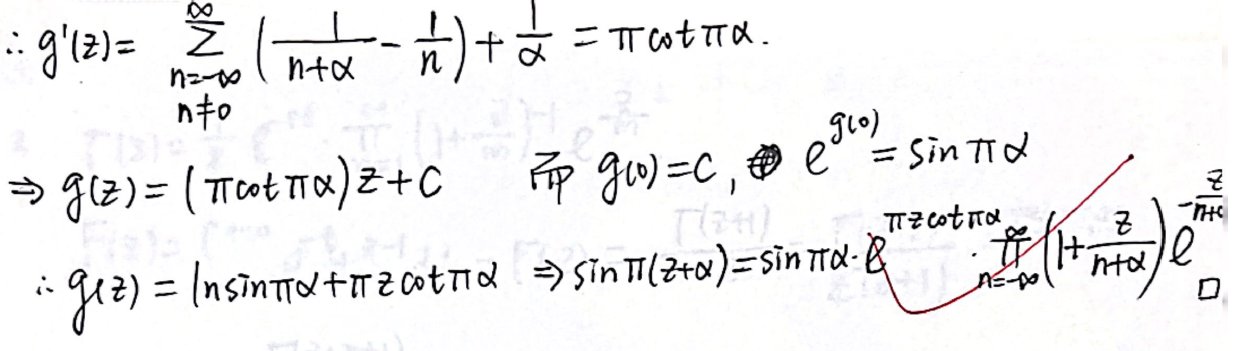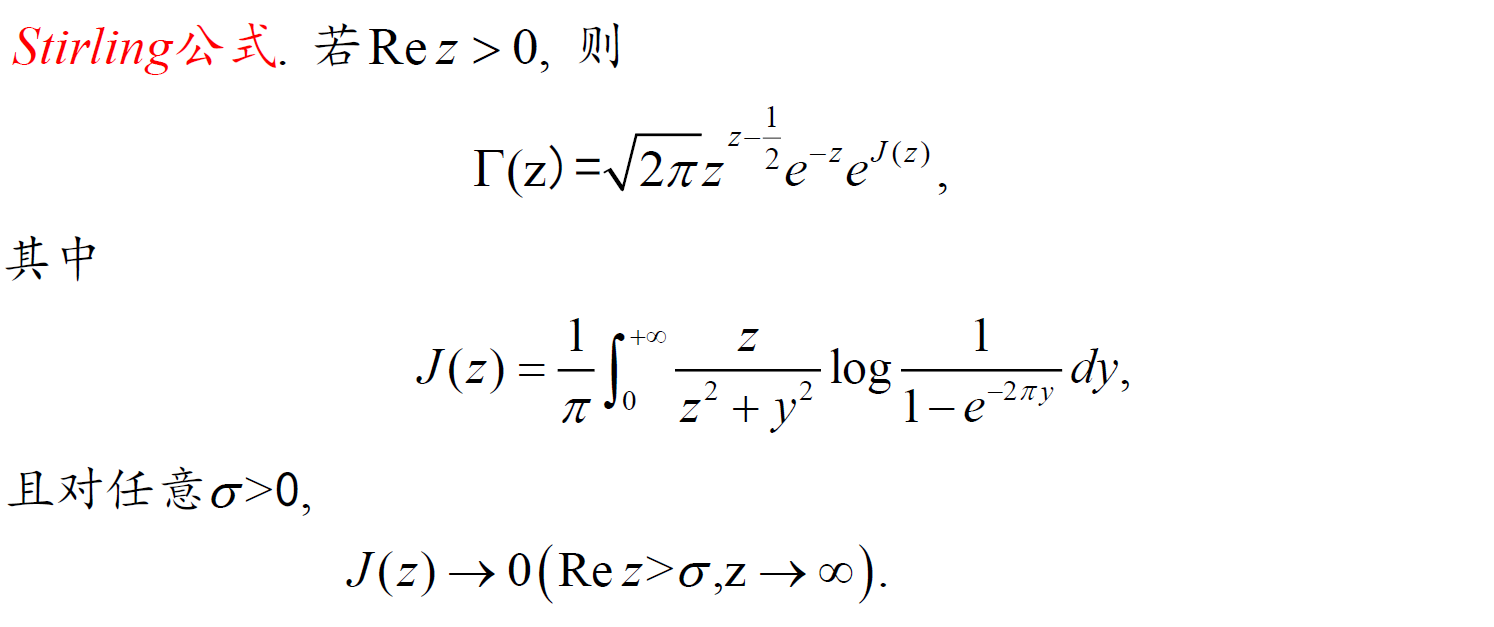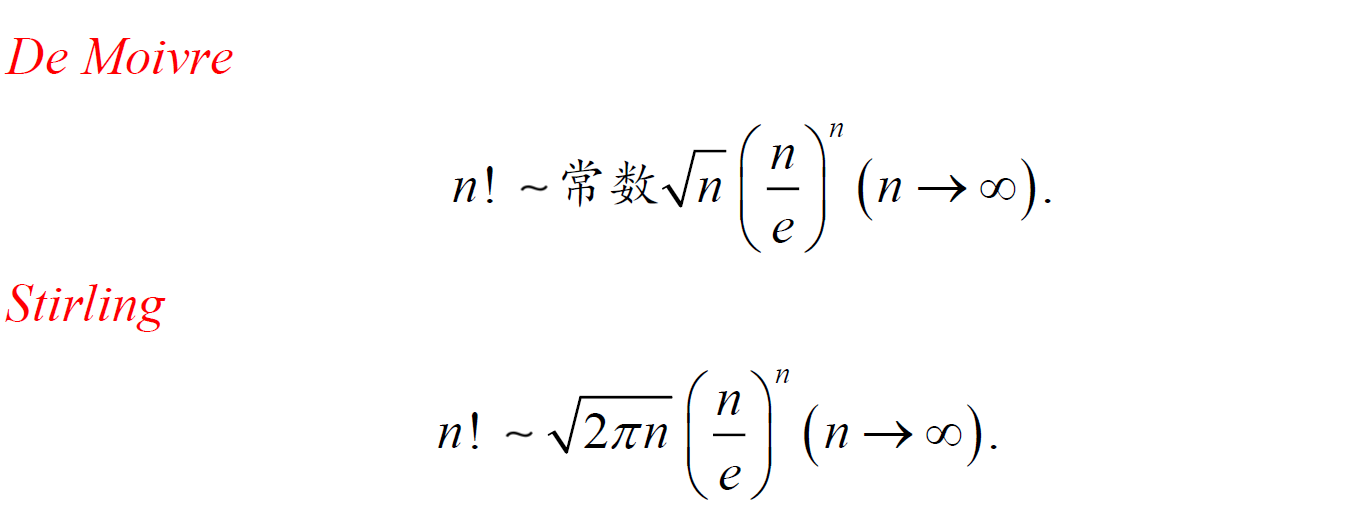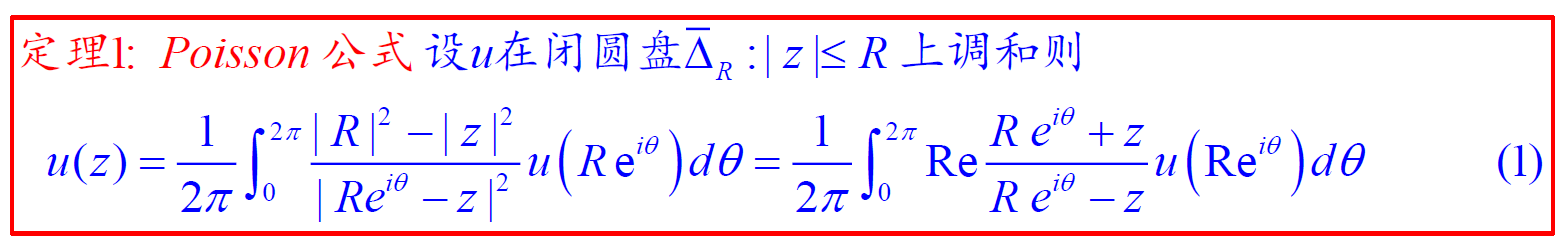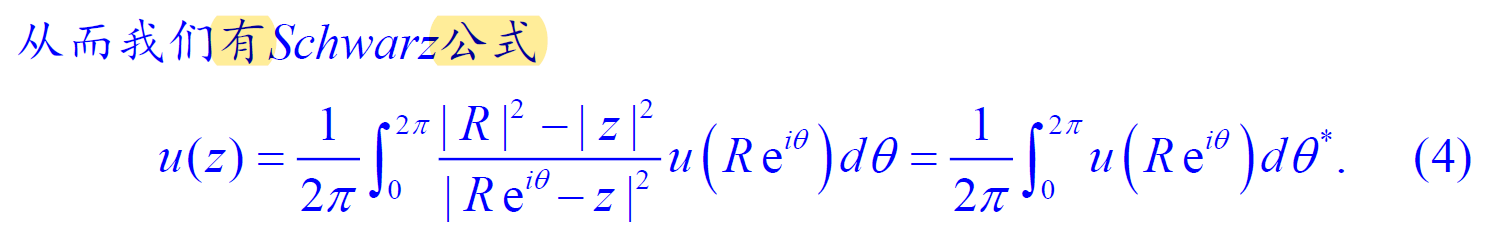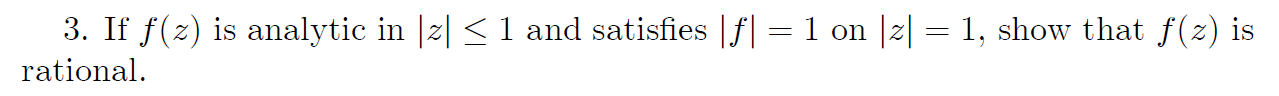断更博主上线!挑战2天学完复分析(2/2)
Ch1 复数与复变函数
1.1 复数的定义及其运算
证明复数不等式
合理利用三角不等式(命题1.1.4,p3)
1.2 复数的几何表示
求几何图形对应的复数方程
- 习题1.2.14

用复数证明几何定理
(感觉不是很重要,就不上图了)
- 例1.2.1
- 例1.2.2
1.3 扩充平面和复数的球面表示

用球面表示求距离/证明性质
貌似都是爆算……
Ch2 全纯函数
2.1 复变函数的导数
2.2 C-R 方程
研究函数可微性
法1:用定义
- 习题2.1.1
法2:用实可微 + C-R方程(\(\Leftrightarrow \frac{\partial f}{\partial \overline{z}}=0\))
- 例2.2.5
- 例2.2.6
研究函数\(f(z)=e^{-|z|^2}\)

证明是/不是调和函数
法1:用定义
法2:用 \(u\in C^2(D),\Delta u=4\frac{\partial ^2 u}{\partial z \partial \overline z}\)
2.4 初等全纯函数
单值解析分支存在性
定理:
(PPT 4,5 - P6)
定理:如果D是不包含原点和无穷远点的单连通域,那么Logz在D上有单值全纯分支。(PPT 4,5 - P9,书本 P54)
根号多值函数的单值解析分支问题
定理:
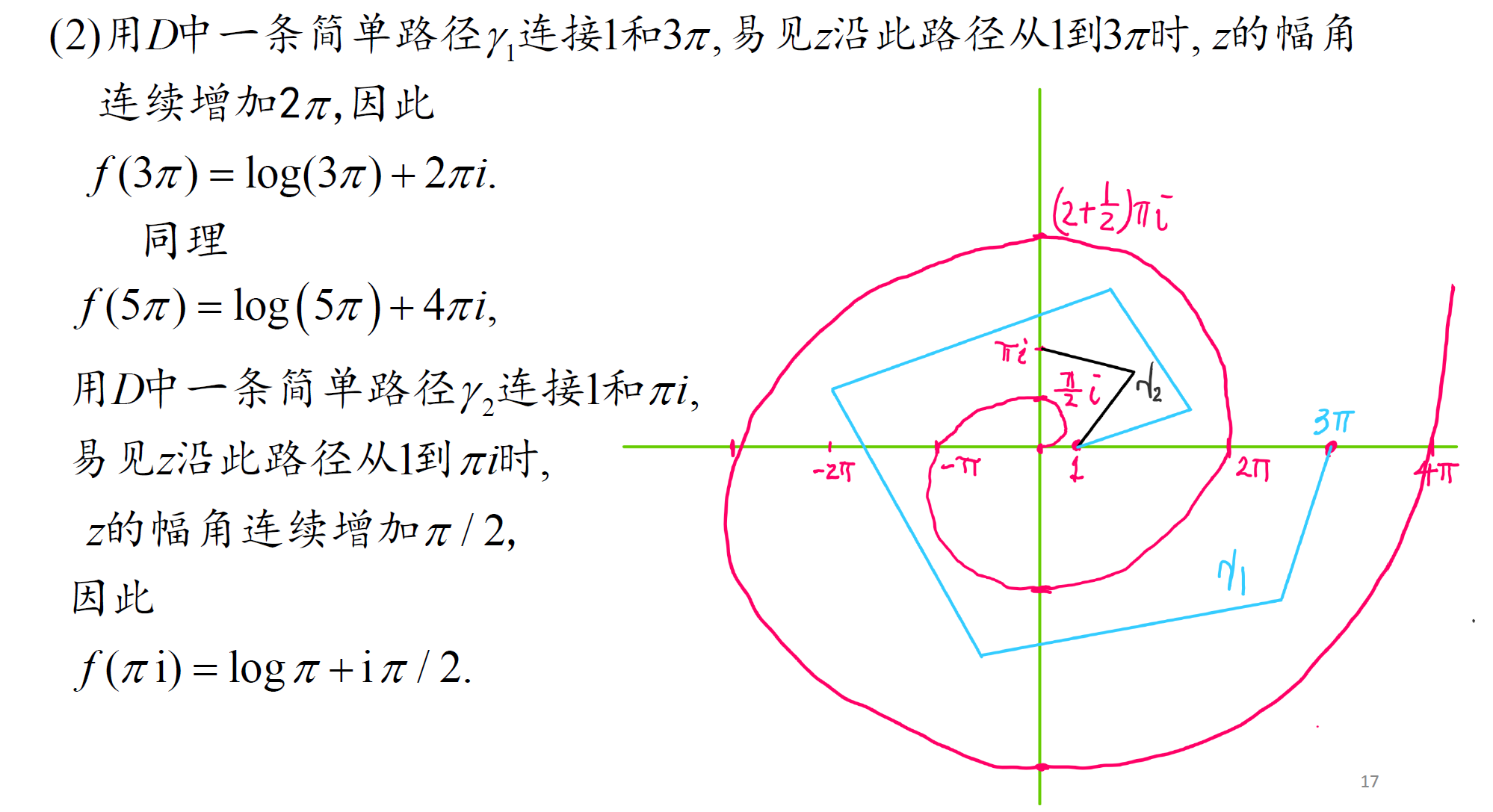
单值解析分支求值
法1:已知一个值,利用简单路径辐角求其他值
法2:直接计算
共形映射区域变换
- 例2.4.5

- 例2.4.6

2.5 分式线性变换
区域变换
法1:利用边界
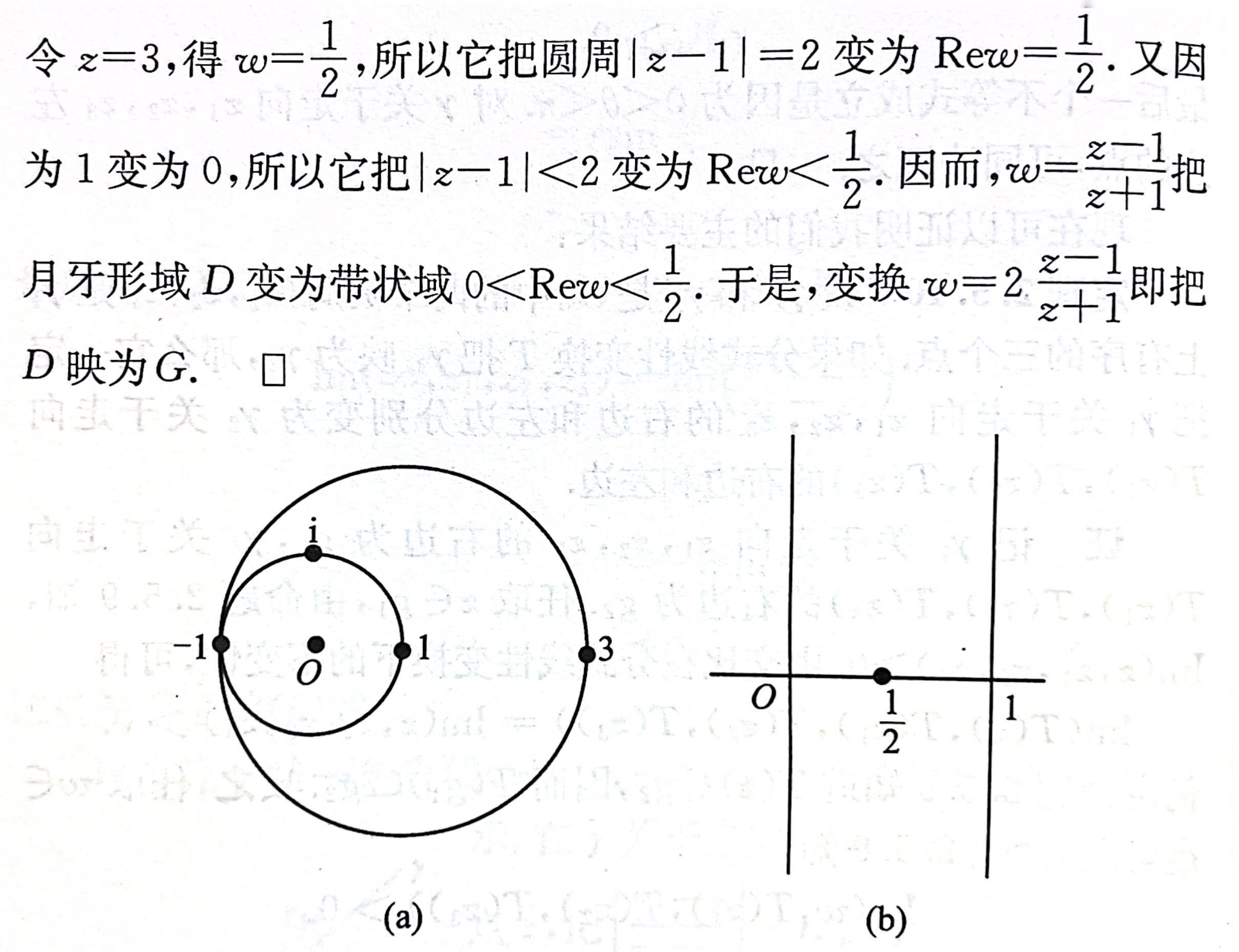
- 例2.5.11

- 习题2.5.3
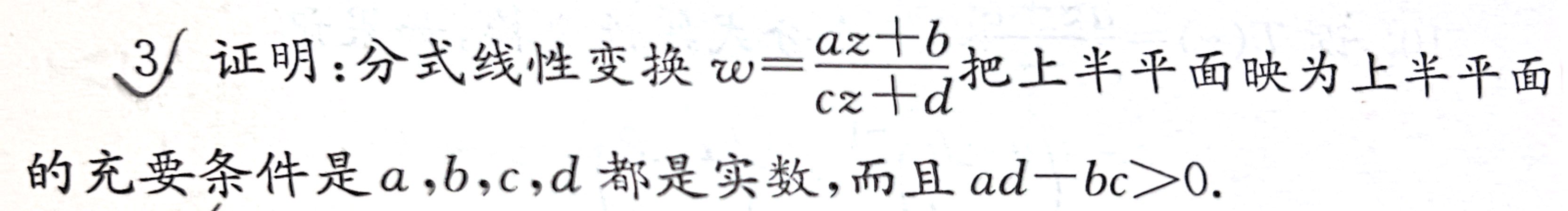
充分性:利用该映射把实轴映为实轴,找 \(z_1,z_2,z_3\rightarrow w_1,w_2,w_3\) 直接算出分式线性变换,再利用唯一性。
法2:利用对称点
- 例2.5.15

- 例2.5.16

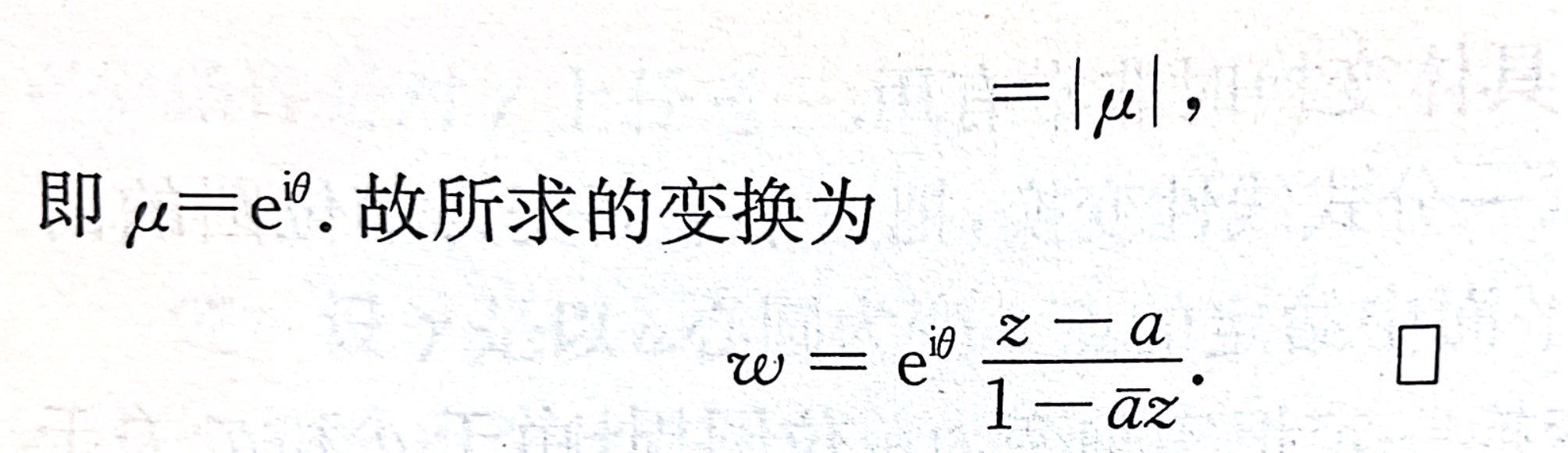
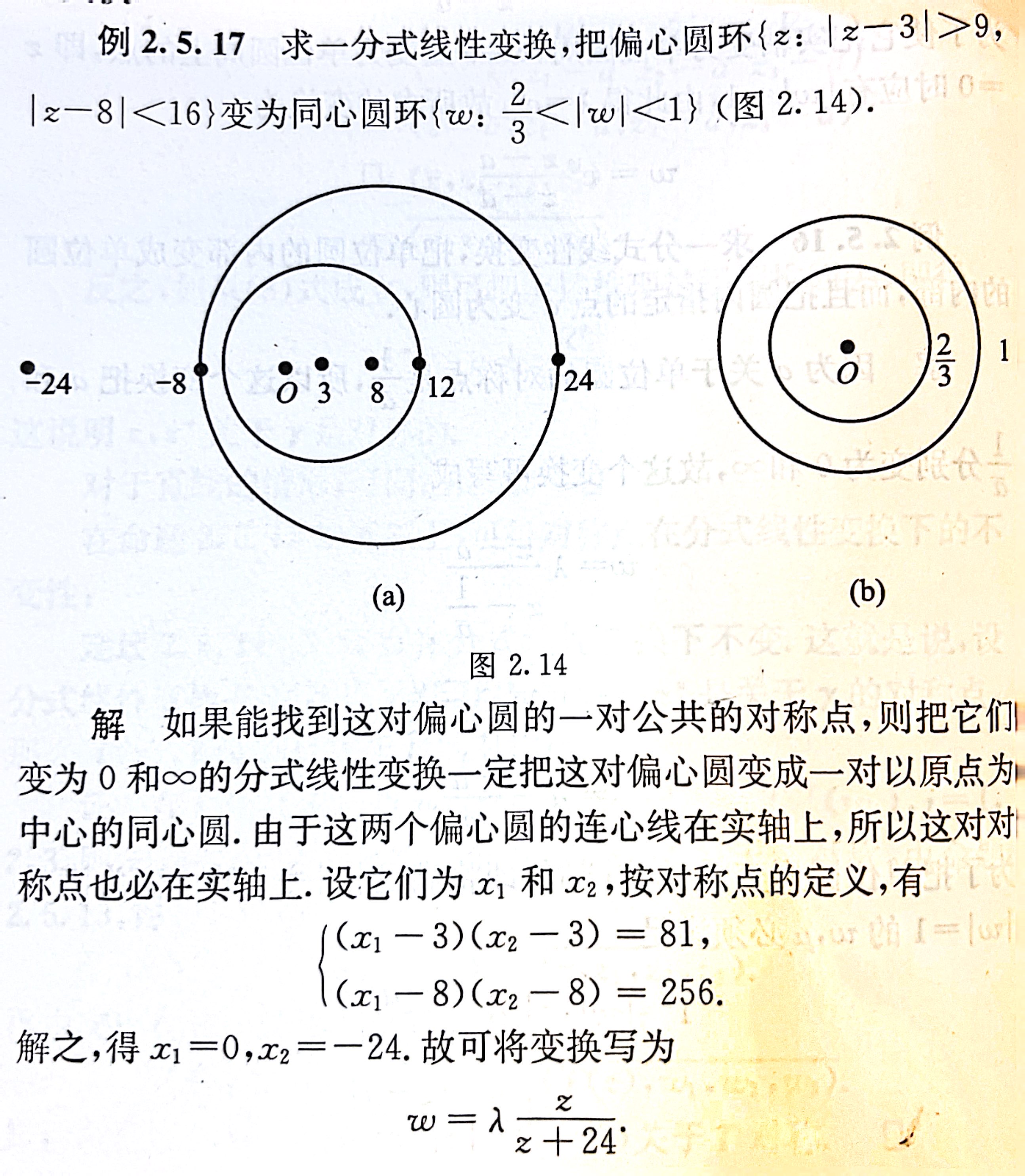
- 例2.5.17
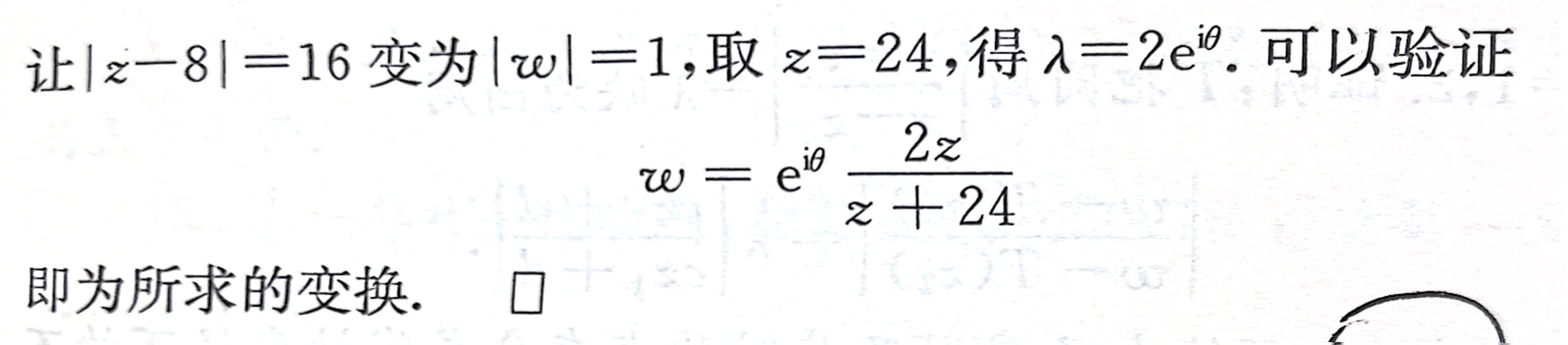
法3:找对应点,待定系数
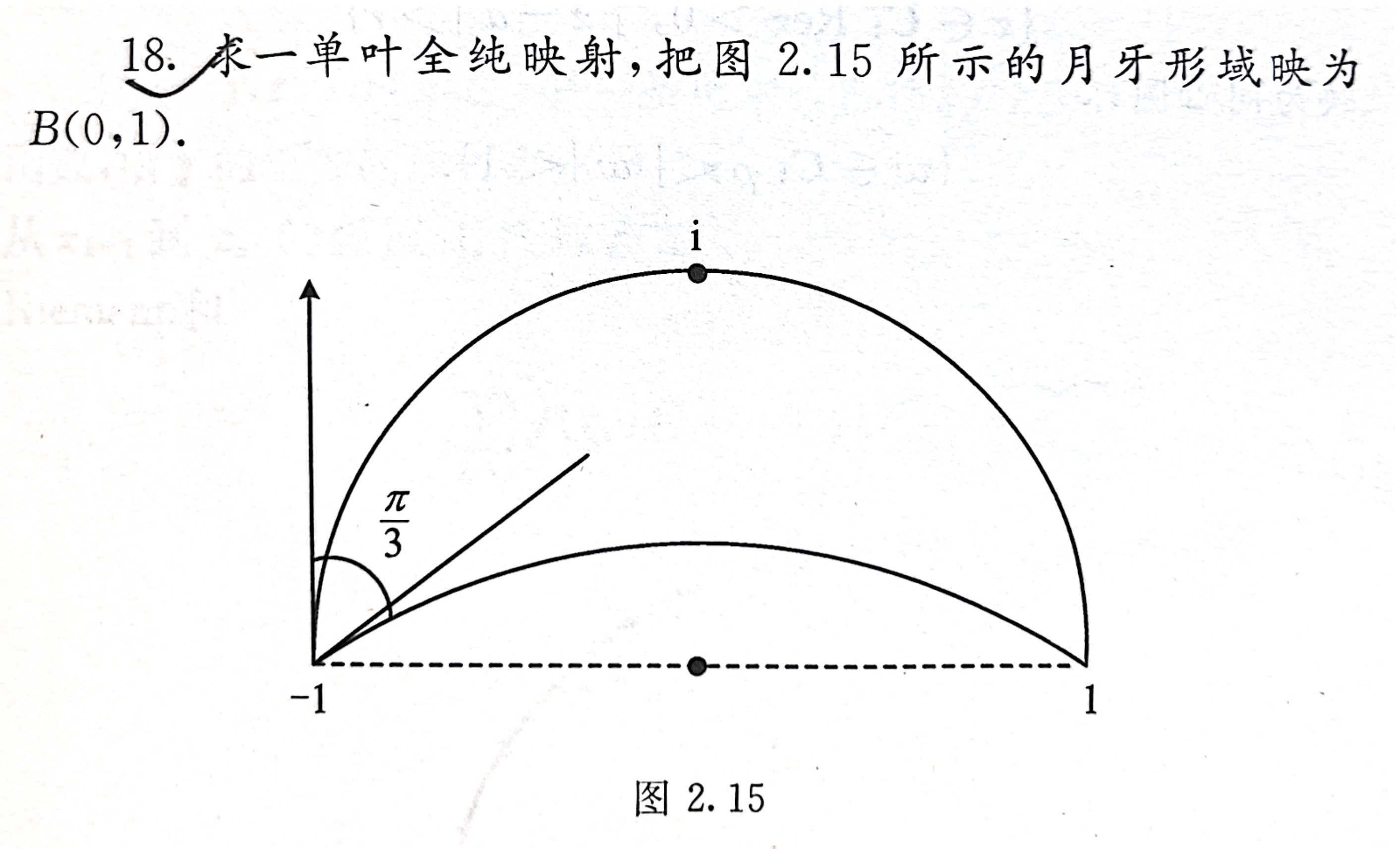
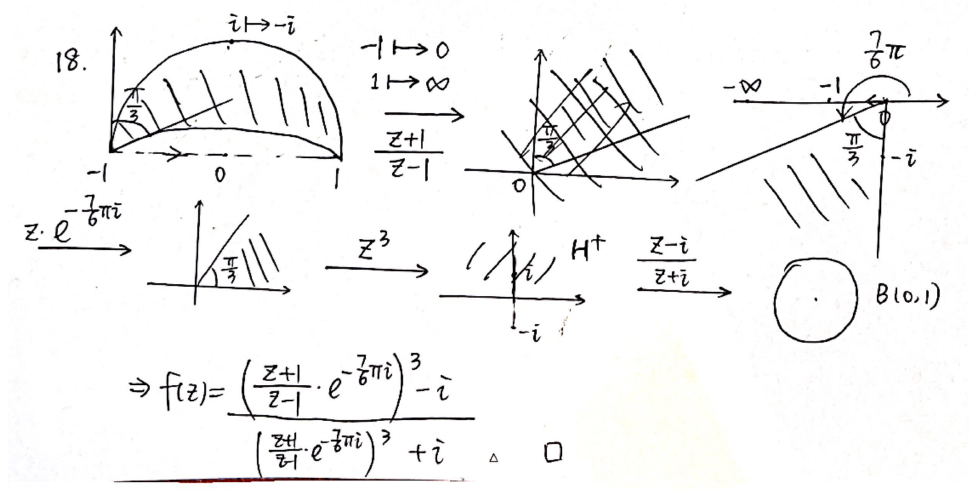
- 习题2.5.20

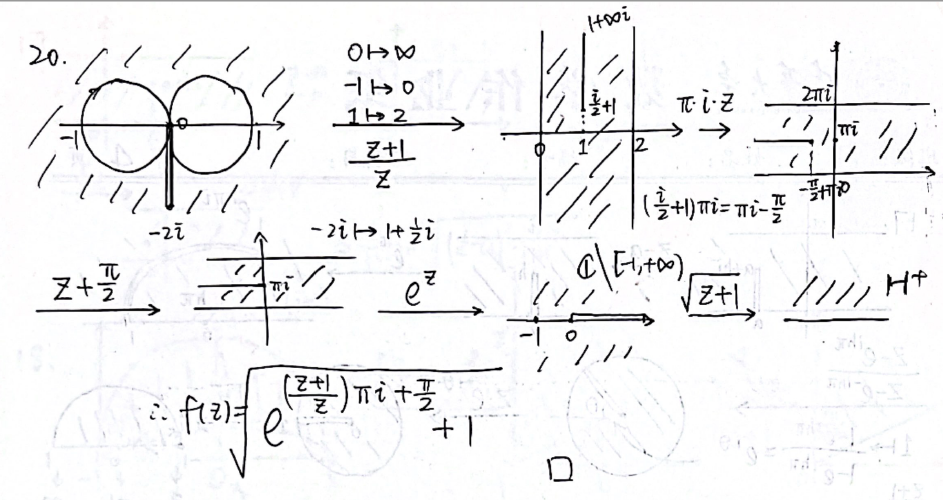
法4:结合共形映射和分式线性变换(不知道怎么归类捏)
- 习题2.5.17


- 习题2.5.18
Ch3 全纯函数的积分表示
3.1 复变函数的积分
计算积分
运用下列公式:
- (换元法,Green 公式)
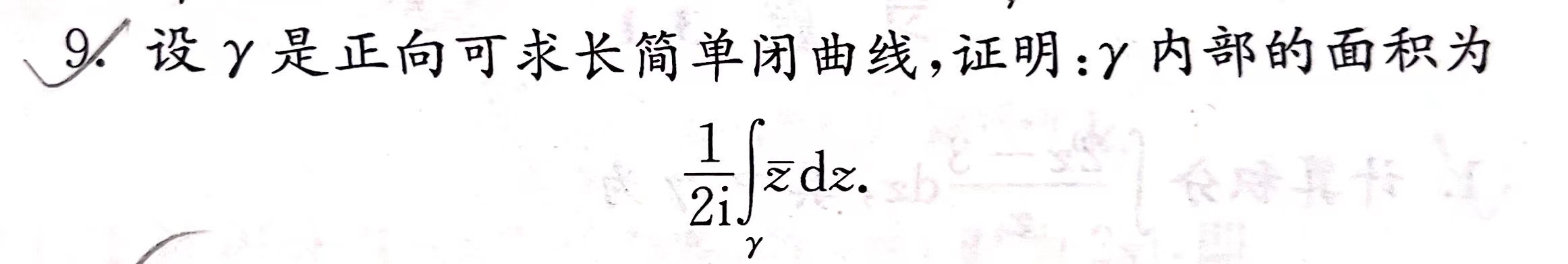
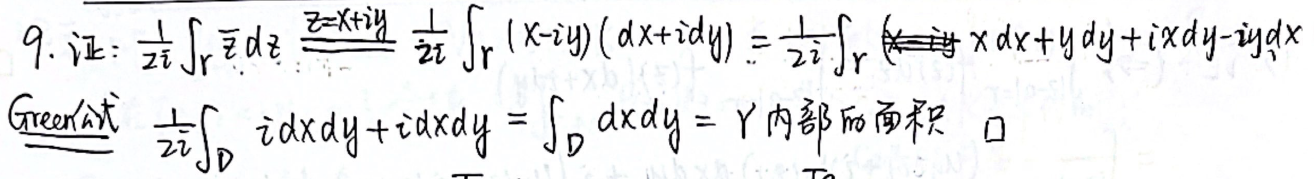
- (换元法,长大不等式,利用 \(\frac{dz}{(z-a)^n}\) 的积分公式)


- (恰当形式)



3.2 Cauchy 积分定理
计算积分
判断:单连通域;全纯函数;(导数连续;)可求长闭曲线。
3.4 Cauchy 积分公式
计算积分
利用 Cauchy 积分公式及其导数形式,把大的闭合曲线用 Cauchy 积分定理转换为小的包含奇点的曲线。
选取合适的曲线,可以在曲线上做极限运算等。
3.5 Cauchy 积分公式的一些重要推论
可以运用的重要推论:
证明整函数是常值函数
结合分式线性变换化为“有界整函数”,运用 Liouville 定理。

证明域上的连续函数全纯
运用 Morera 定理,讨论曲线的性质。


(事实上要作逼近,但是太烦了不如省略!)(溜)
Ch4 全纯函数的 Taylor 展开及其应用
4.1 Weierstrass 定理
证明级数内闭一致收敛
利用 Weierstrass 定理:
注意闭集的性质(最大模),和 内闭一致收敛 \(\Leftrightarrow\) 在域中任何闭圆盘上收敛。
4.2 幂级数
利用已知级数求给定级数


(最后一步反证法)
4.3 全纯函数的 Taylor 展开
求 Taylor 展开式
法1:利用 Taylor 展开定理

法2:利用反函数的展开求反 / 导数的展开积分
证明函数全纯
4.4 辐角原理和 Rouche 定理
求零点个数
法1:利用 Rouche 定理
注意选取函数 \(f(x),g(x)\),记得做必要的放缩。
- 例4.4.12

- 例4.4.13
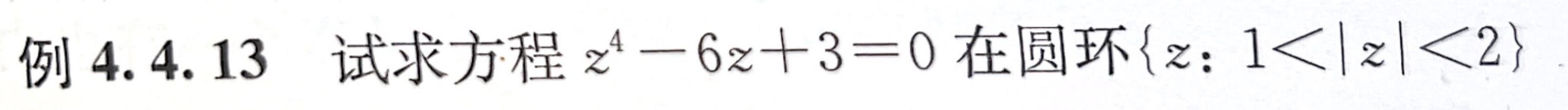

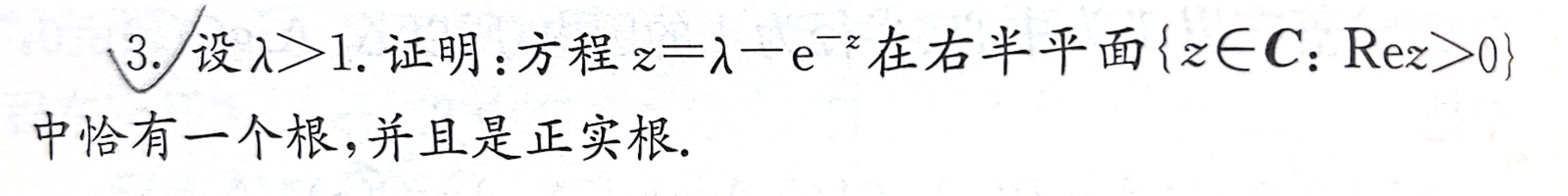

法2:利用辐角原理
先取简单闭曲线,证明简单闭曲线上没有零点,再计算围绕简单闭曲线走一圈的辐角变化,用辐角原理解零点个数。
- 例4.4.14
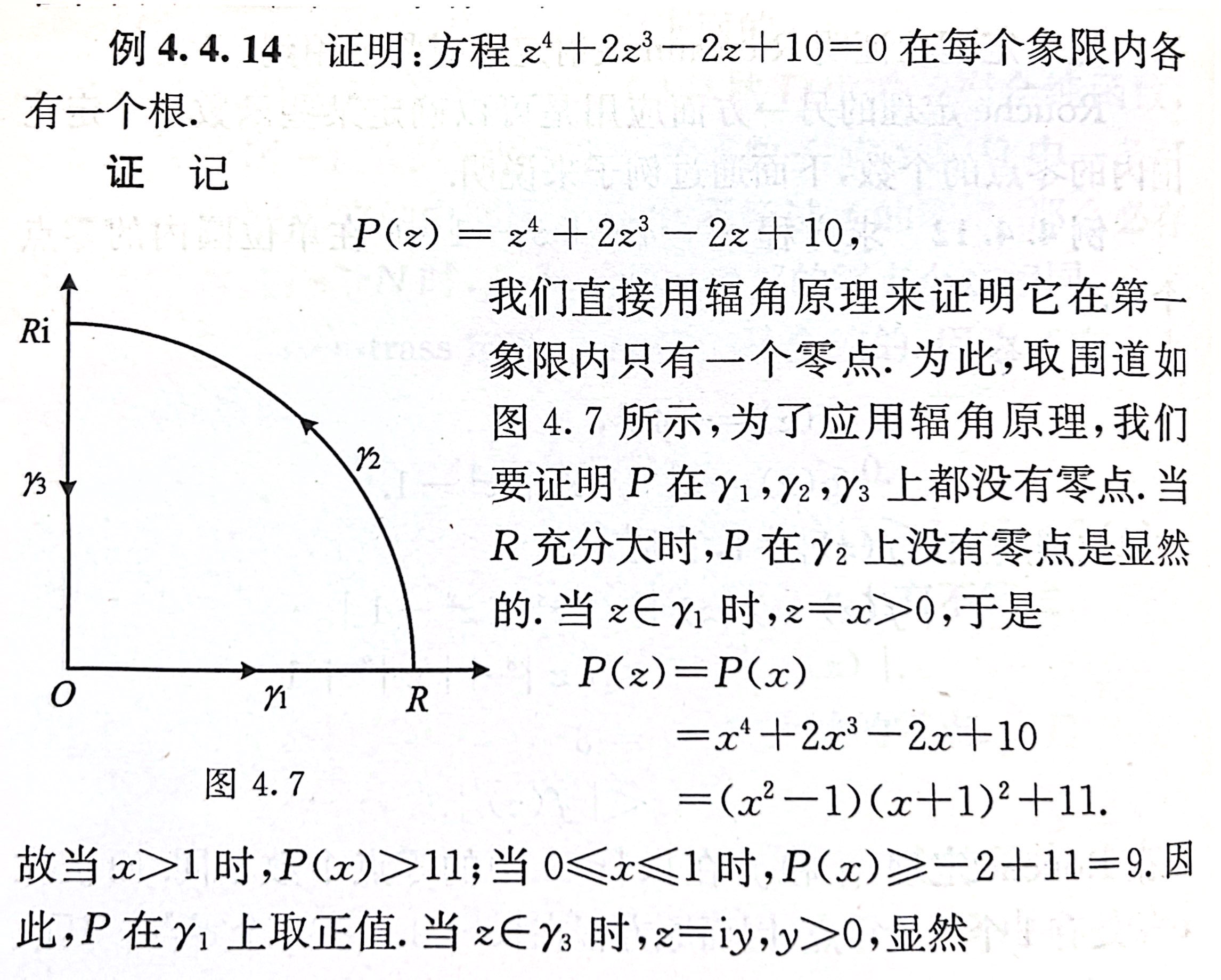


法3:利用 Hurwitz定理
把数学量转化为辐角
与定理4.4.4相关的推论


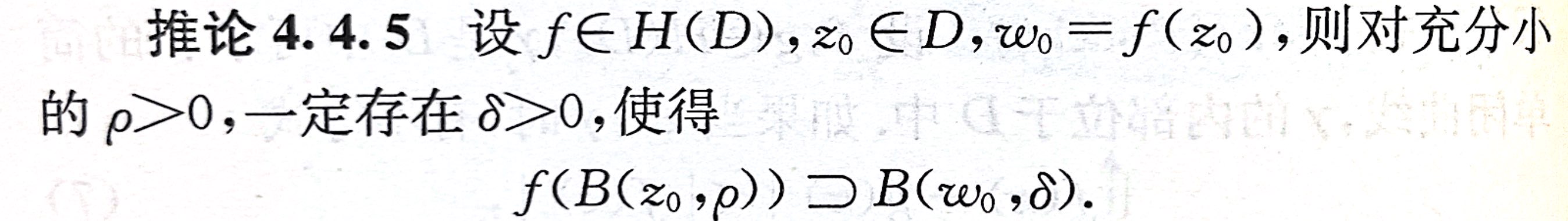
4.5 最大模原理和 Schwarz 引理
Schwarz 引理和分式线性变换的应用
可以使用的定理:
关键是灵活选取分式线性变换!(哭死,我不会)
全纯自同构的应用
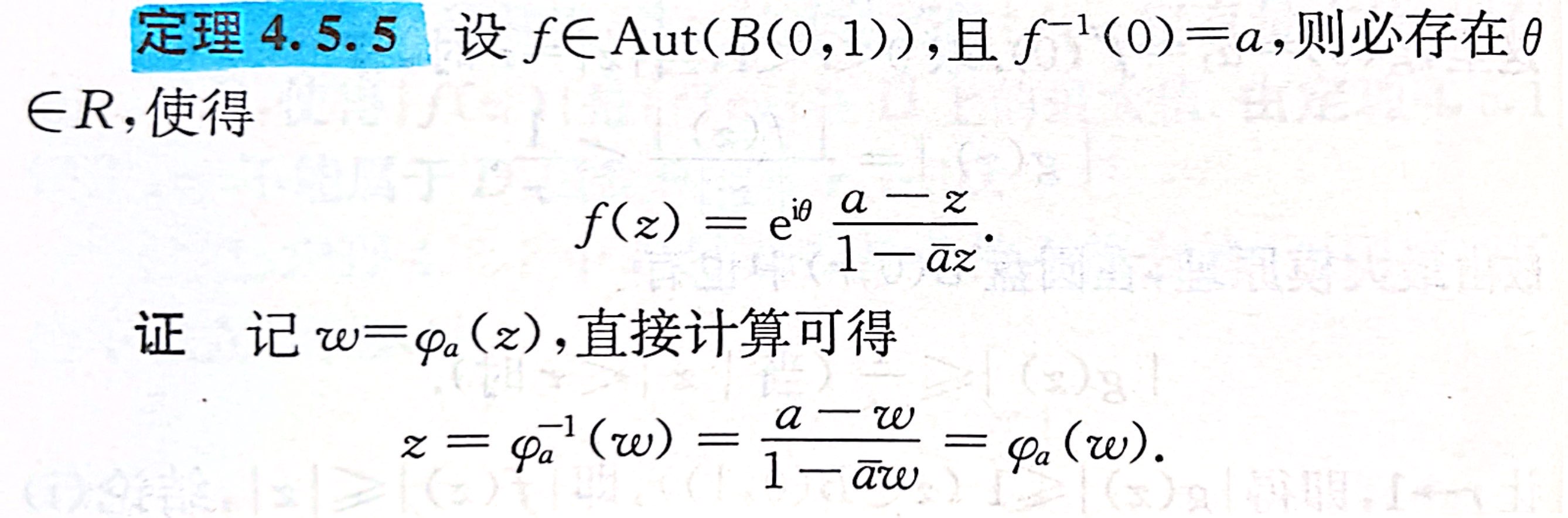

分类讨论。当内部没有零点的时候,由最大模定理,是常函数 \(e^{i\theta}\);当内部有零点的时候,设零点 \(a_1,...,a_t\) 重数分别为 \(k_1,...,k_t\) ,先运用 \(a_1\) 的全纯自同构 \(\varphi_{a_1}\),得到

- (利用了最大模定理的证明思想)
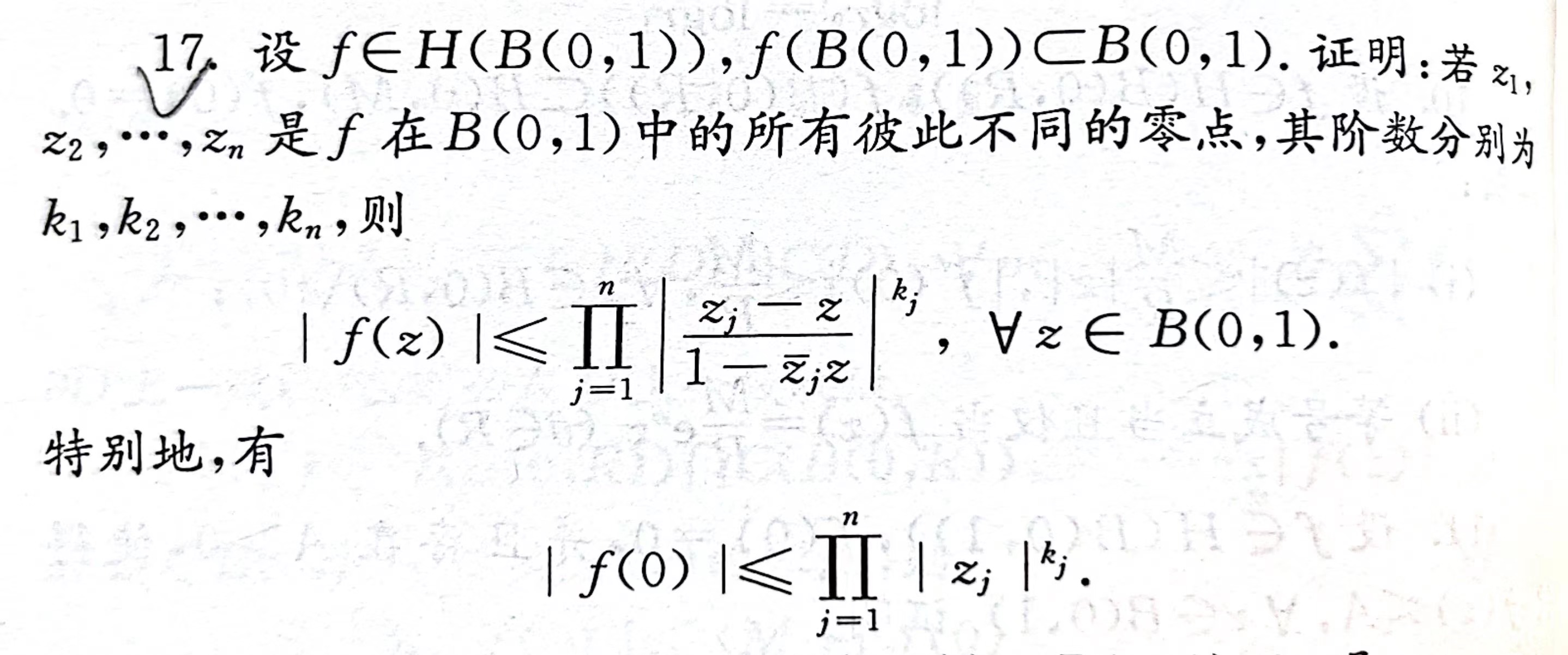

Ch5 全纯函数的 Laurent 展开及其应用
5.1 全纯函数的 Laurent 展开
求函数的 Laurent 展开


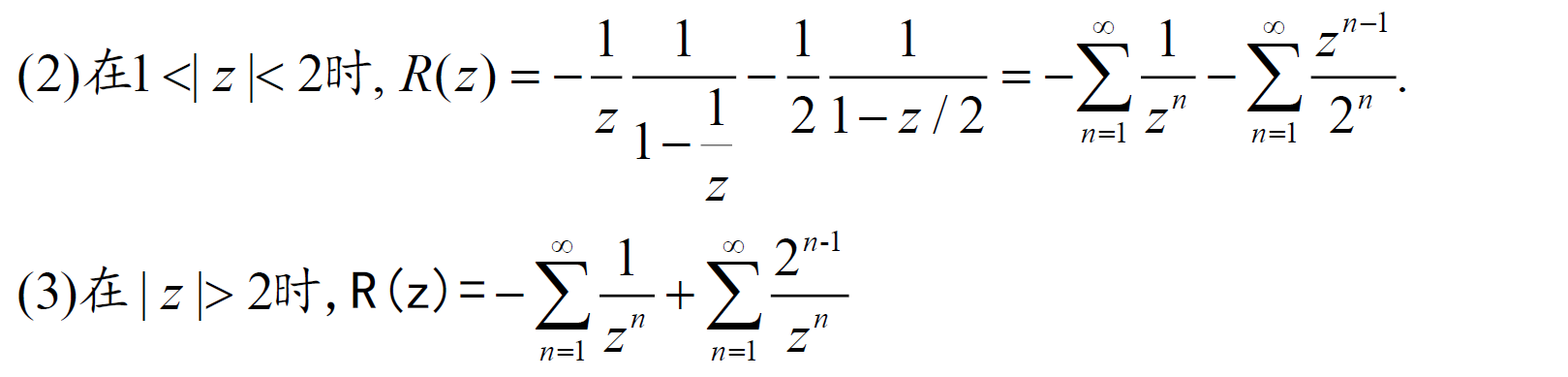
- (先解出具体表达式,确定全纯的圆/圆环)
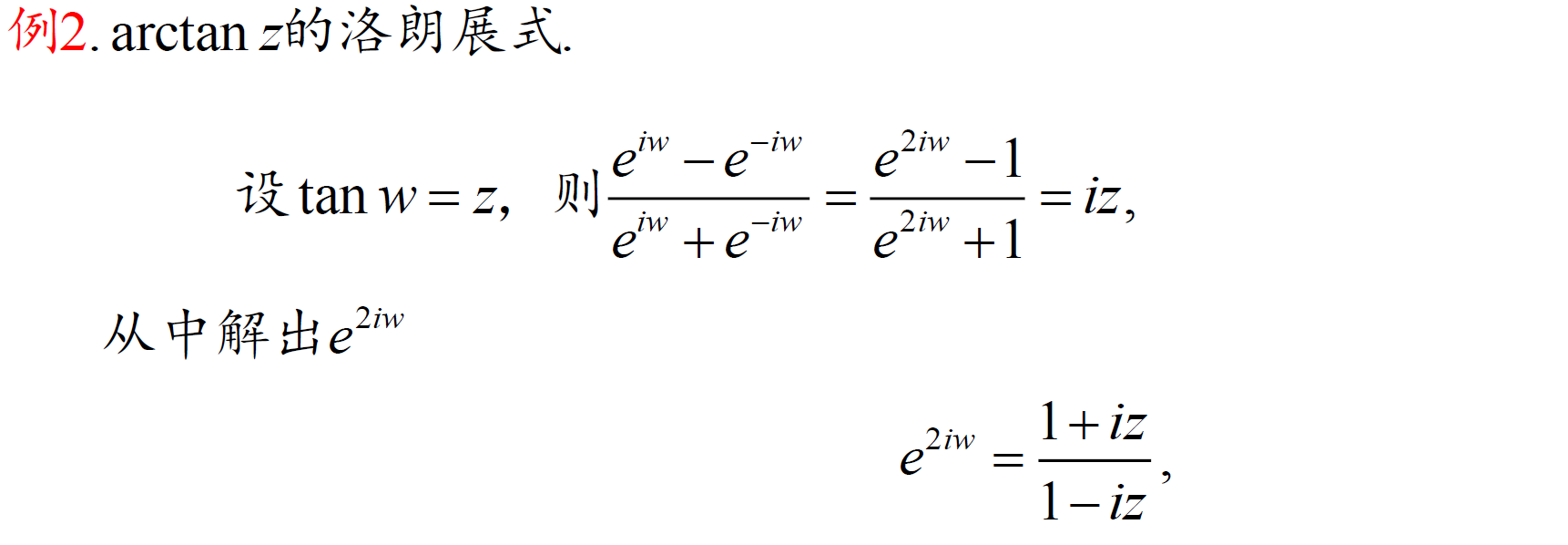


5.2 孤立奇点及其分类
- 可去奇点 \(\Leftrightarrow\) 函数在点附近有界
- 极点 \(\Leftrightarrow\) 倒数函数的零点
- m 阶极点 \(\Leftrightarrow\) 倒数函数的 m 阶零点 \(\Leftrightarrow\) 展开式全纯部分最低 -m 阶
- 本性奇点 \(\Rightarrow\) Weierstrass + Picard


5.3 整函数与亚纯函数
没太能 get 到题型,大家鉴赏一点题目吧(
5.4 留数定理 / 残数定理
计算留数
法1:乘以 \((z-a)^n\),运用求导
法2:一重极点 + 分式型
法3:本性奇点或易于展开的形式:直接展开
计算积分

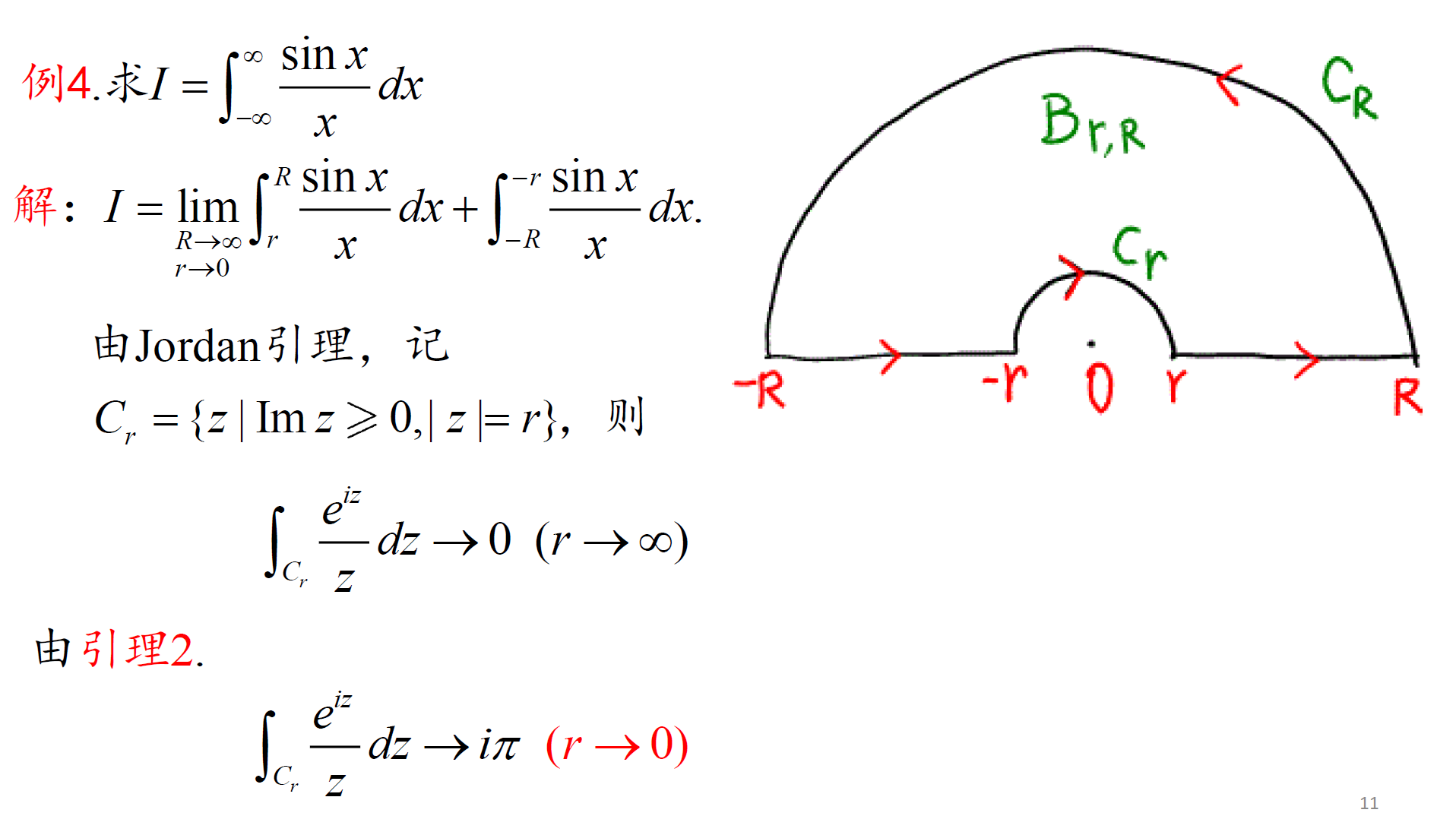
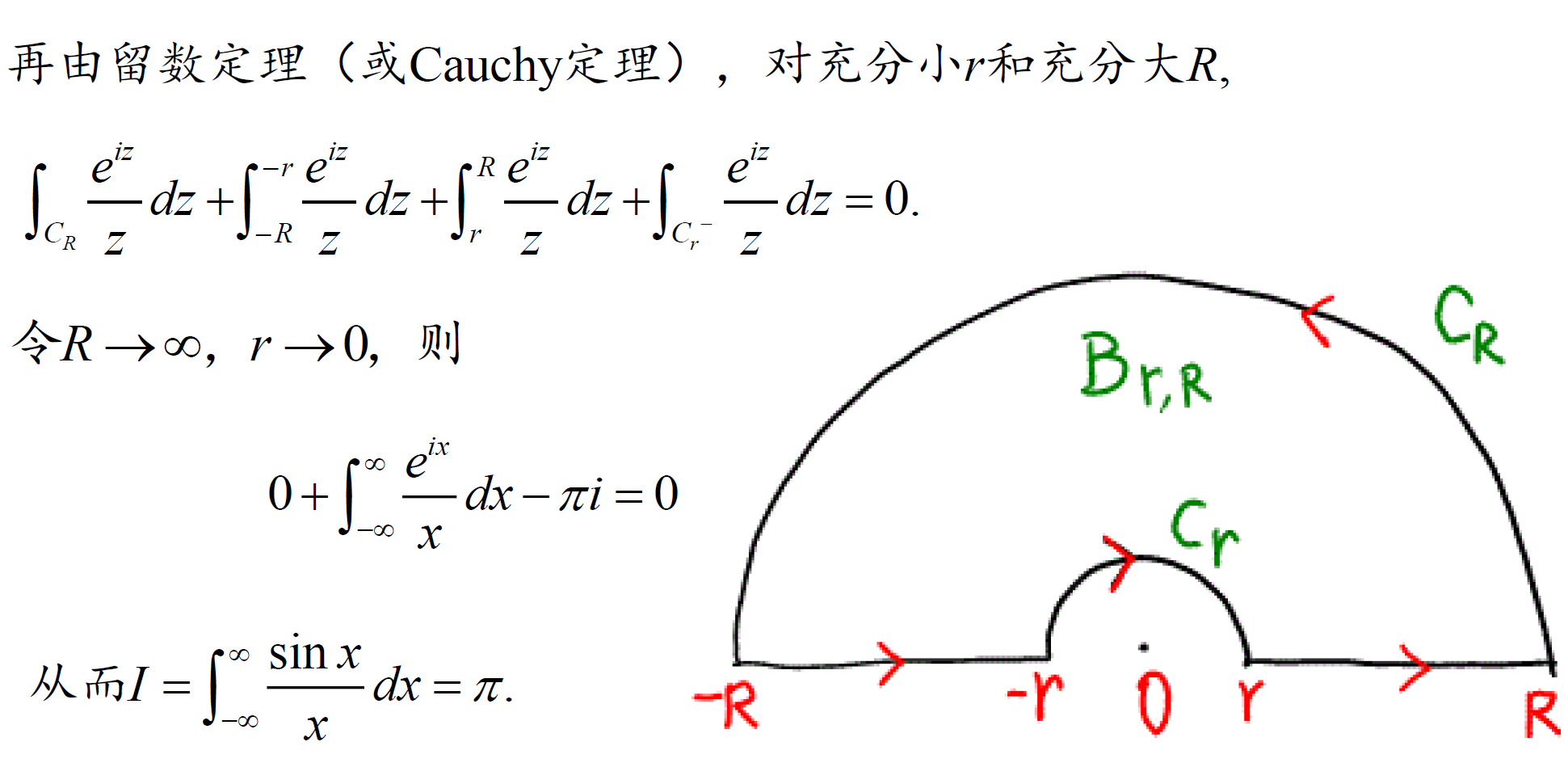
5.5 利用留数定理计算定积分
\(\int_{-\infty}^\infty f(x)dx\) 型积分
\(\int_{-\infty}^\infty R(\cos\theta,\sin\theta)d\theta\) 型积分
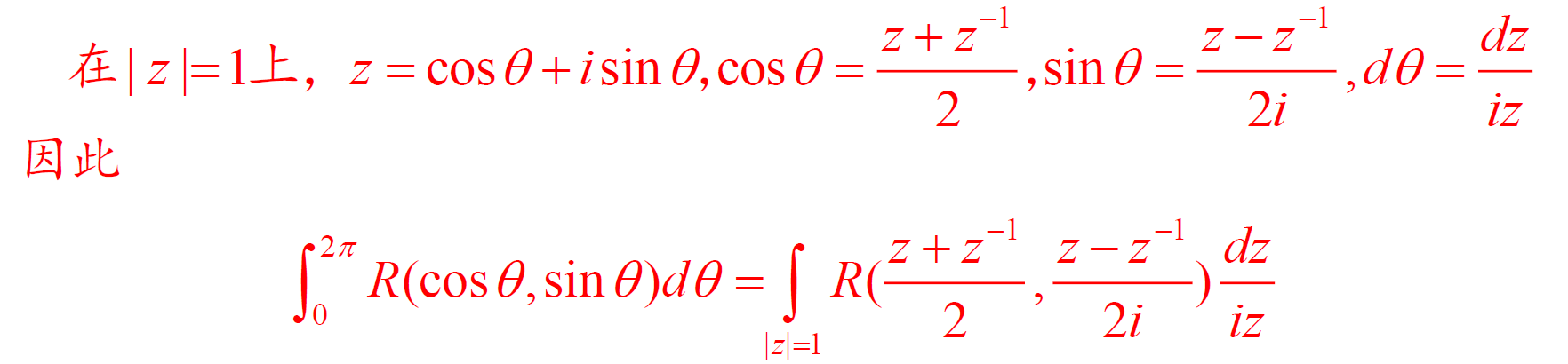
嘛玩意儿啊,其他两类先不整理了(
5.6 整亚纯函数的部分分式展开 & Mittag-Leffler定理
意外地发现 zgy 这张 PPT 的文本框旋转了一点 0 0
应用公式(1)-(3)解题

题解略。都利用了上面的公式拼凑想要的式子,因此核心在于记忆公式。
5.7 无穷乘积
略显简单,只需要用定义 + 等价条件即可。
5.8 函数项无穷乘积与典型乘积
证明存在满足取值条件的函数
构造(可待定系数) + 证明(收敛)
证明某函数 = 某级数
5.9 \(\Gamma\) 函数的无穷乘积定义
牢记几条重要公式:
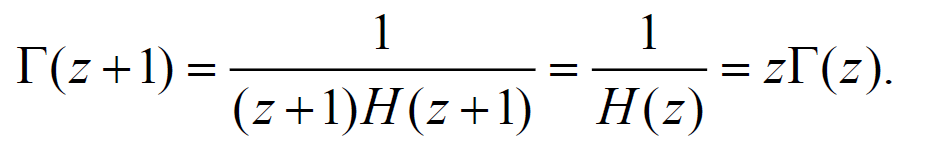
(\(\Gamma\) 函数是阶乘的推广)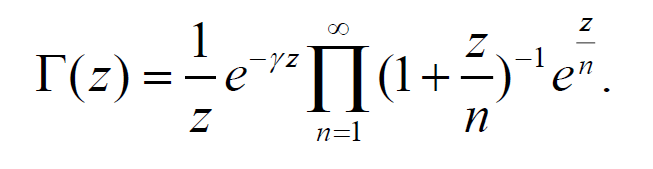
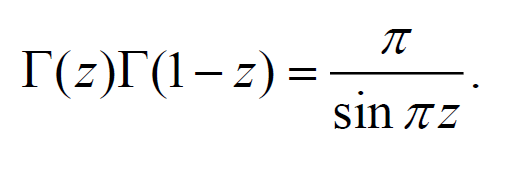
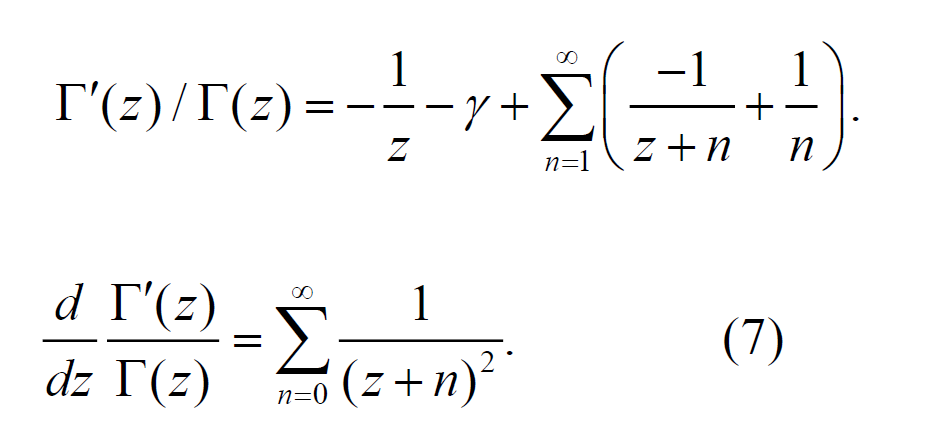
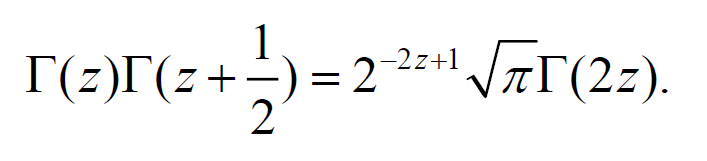
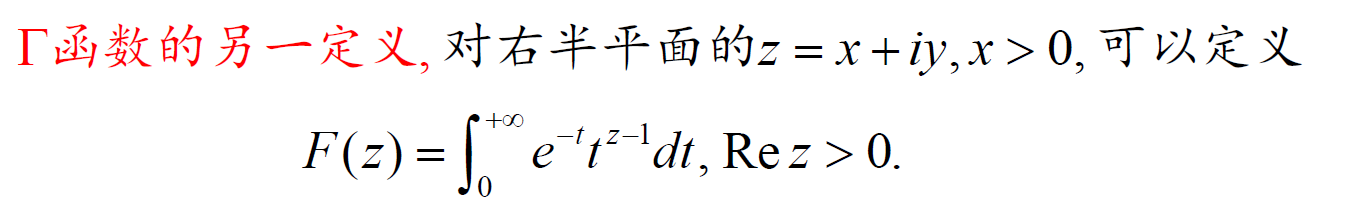
5.10 Stirling 公式和 \(\Gamma\) 函数定义的等价性
Ch6 调和函数初步和全纯开拓
6.1 调和函数基本性质
TODO
6.3 Poisson 公式 & 6.4 Schwarz 定理
运用公式解题
就嗯套公式……
运用 Schwarz 定理进行延拓 / 证明调和
参见 6.5 节定理的证明方式
6.5 Schwarz对称开拓原理
利用对称开拓原理解题
核心思路都是选取合适的开拓原理在某一步开拓,但开拓都是为证明全局服务 0 0