对于 200 个观察，\(\beta\) 的估计是巨大的，标准差相对较小！

让我们深入探讨这一点。我在犹他大学数学系的超级计算机上进行了一些数值实验（译注：实际上，普通家用电脑也能应付）。下面是一个辅助函数，用于通过 garchFit()（在计算过程中屏蔽所有 garchFit() 的输出）来提取特定拟合的系数和标准差。

getFitData <- function(x,
                       cond.dist = "QMLE",
                       include.mean = FALSE,
                       ...)
{
    args <- list(...)
    args$data = x
    args$cond.dist = cond.dist
    args$include.mean = include.mean

    log <- capture.output(
        {
            fit <- do.call(garchFit, args = args)
        })

    res <- coef(fit)
    res[paste0(names(fit@fit$se.coef), ".se")] <- fit@fit$se.coef
    return(res)
}

第一个实验是在每个可能的截止点计算该特定序列的系数。

(在编写此文档时，不会评估以下代码块。我已将结果保存在 Rda 文件中。对于涉及并行计算的每个代码块都是如此。我在犹他大学数学系的超级计算机上执行了这些计算，在这里保存结果。)

library(doParallel)

set.seed(110117)

cl <- makeCluster(detectCores() - 1)
registerDoParallel(cl)

x <- garchSim(
    garchSpec(
        model = list(
            alpha = 0.2, beta = 0.2, omega = 0.2)),
    n.start = 1000, n = 1000)

params <- foreach(
    t = 50:1000,
    .combine = rbind,
    .packages = c("fGarch")) %dopar%
    {
        getFitData(x[1:t])
    }
rownames(params) <- 50:1000

下面我绘制这些系数，以及对应于两倍标准差的区域。该区域应大致对应 95％ 的置信区间。

params_df <- as.data.frame(params)
params_df$t <- as.numeric(rownames(params))
ggplot(params_df) +
    geom_line(
        aes(x = t, y = beta1)) +
    geom_hline(
        yintercept = 0.2, color = "blue") +
    geom_ribbon(
        aes(x = t,
            ymin = beta1 - 2 * beta1.se,
            ymax = beta1 + 2 * beta1.se),
        color = "grey", alpha = 0.5) +
    ylab(expression(hat(beta))) +
    scale_y_continuous(
        breaks = c(0, 0.2, 0.25, 0.5, 1)) +
    coord_cartesian(ylim = c(0, 1))

这是一幅令人震惊的画面（但不是我见过的最令人震惊的画面，这是最好的案例之一）。请注意，置信区间无法覆盖 \(\beta = 0.2\) 的真实值，直到大约 375 个数据点。这些间隔本应该在大约 95％ 的时间内包含真实值！除此之外，置信区间相当大。

让我们看看其他参数的行为。

library(reshape2)
library(plyr)
library(dplyr)

param_reshape <- function(p)
{
    p <- as.data.frame(p)
    p$t <- as.integer(rownames(p))

    pnew <- melt(
        p, id.vars = "t", variable.name = "parameter")

    pnew$parameter <- as.character(pnew$parameter)
    pnew.se <- pnew[grepl("*.se", pnew$parameter), ]
    pnew.se$parameter <- sub(".se", "", pnew.se$parameter)
    names(pnew.se)[3] <- "se"
    pnew <- pnew[!grepl("*.se", pnew$parameter), ]

    return(
        join(
            pnew, pnew.se,
            by = c("t", "parameter"),
            type = "inner"))
}

ggp <- ggplot(
    param_reshape(params),
    aes(x = t, y = value)) +
    geom_line() +
    geom_ribbon(
        aes(ymin = value - 2 * se,
            ymax = value + 2 * se),
        color = "grey",
        alpha = 0.5) +
    geom_hline(yintercept = 0.2, color = "blue") +
    scale_y_continuous(
        breaks = c(0, 0.2, 0.25, 0.5, 0.75, 1)) +
    coord_cartesian(ylim = c(0, 1)) +
    facet_grid(. ~ parameter)

print(ggp + ggtitle("NLMINB Optimization"))

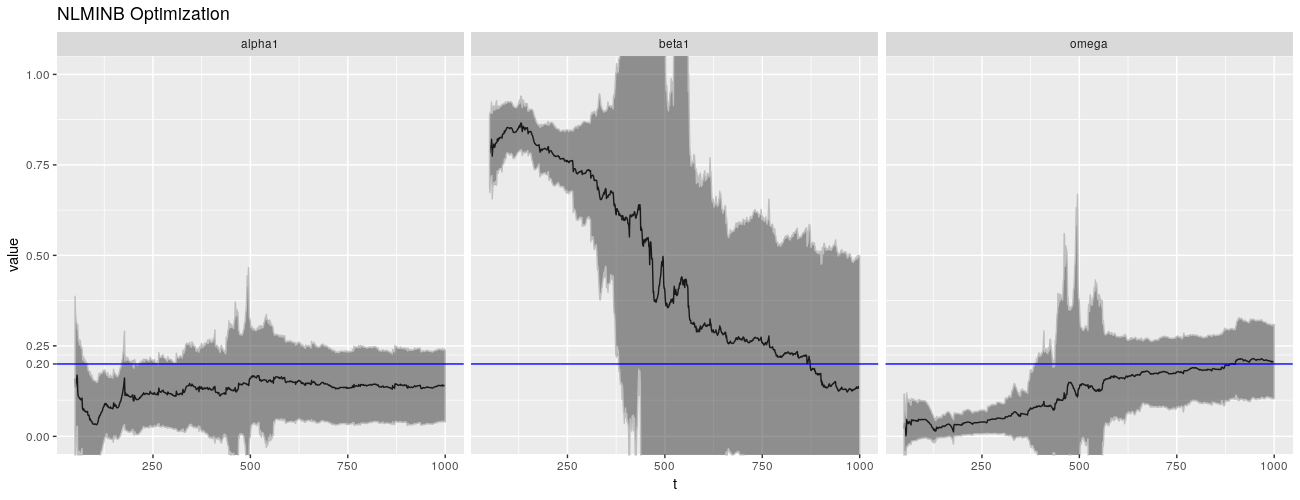
这种现象不仅限于 \(\beta\)，\(\omega\) 也表现出不良行为。(\(\alpha\) 也不是很好，但要好得多。)

这种行为并不罕见，这是典型的。下面是使用不同种子生成的类似序列的图。