3 探索性数据分析

时间序列很长（有 265 年！）。我们可以将时间序列的全部（265 年）以及前 50 年的数据可视化，以获得该时间系列的直观感受。

3.1 使用 COWPLOT 可视化太阳黑子数据

我们将创建若干 ggplot 对象并借助 cowplot::plot_grid() 把这些对象组合起来。对于需要缩放的部分，我们使用 tibbletime::time_filter()，可以方便的实现基于时间的过滤。

p1 <- sun_spots %>%
    ggplot(aes(index, value)) +
    geom_point(
        color = palette_light()[[1]], alpha = 0.5) +
    theme_tq() +
    labs(title = "From 1749 to 2013 (Full Data Set)")

p2 <- sun_spots %>%
    filter_time("start" ~ "1800") %>%
    ggplot(aes(index, value)) +
    geom_line(color = palette_light()[[1]], alpha = 0.5) +
    geom_point(color = palette_light()[[1]]) +
    geom_smooth(method = "loess", span = 0.2, se = FALSE) +
    theme_tq() +
    labs(
        title = "1749 to 1800 (Zoomed In To Show Cycle)",
        caption = "datasets::sunspot.month")

p_title <- ggdraw() + 
    draw_label(
        "Sunspots",
        size = 18,
        fontface = "bold",
        colour = palette_light()[[1]])

plot_grid(
    p_title, p1, p2,
    ncol = 1,
    rel_heights = c(0.1, 1, 1))

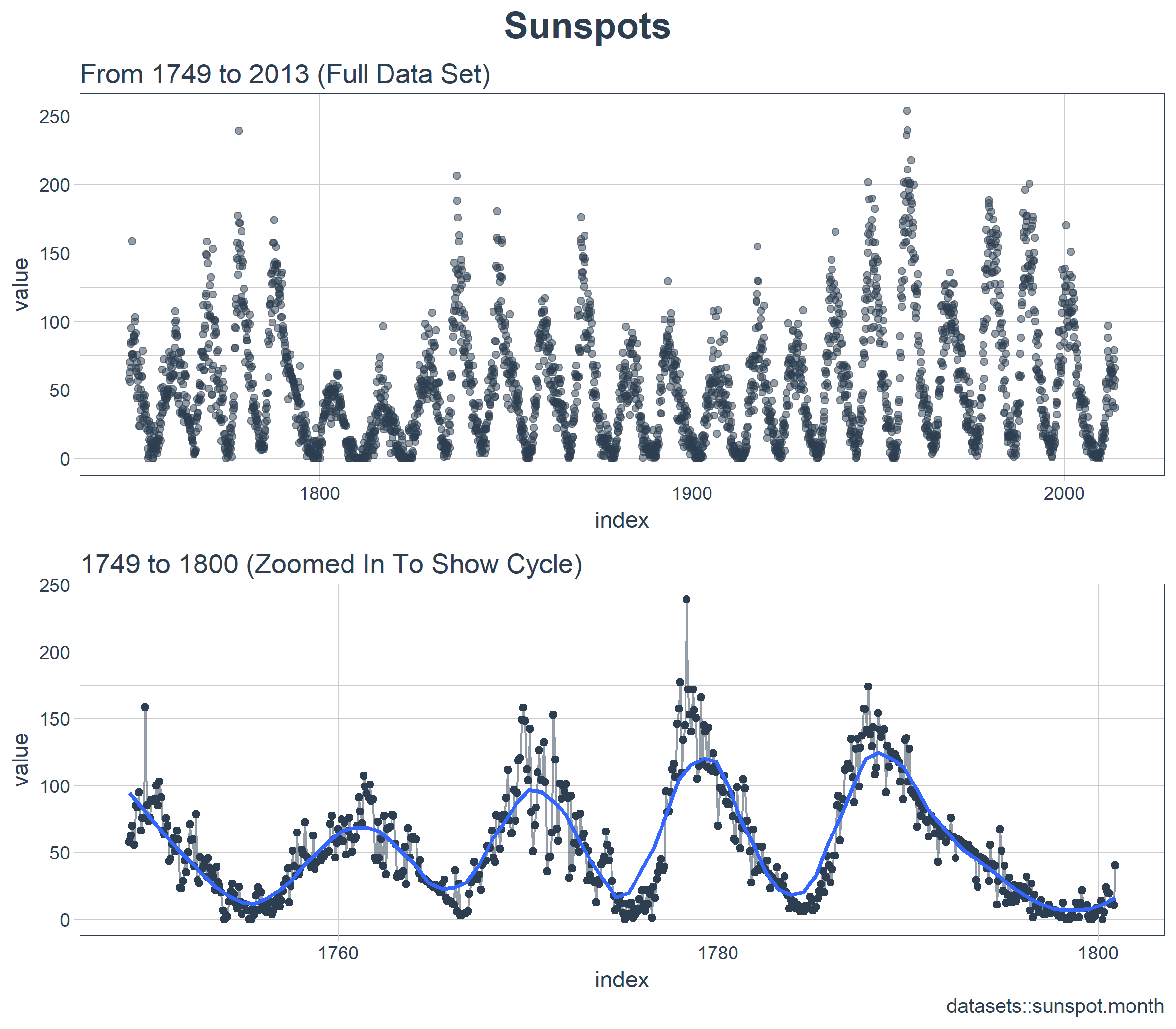
乍一看，这个时间序列应该很容易预测。但是，我们可以看到，周期（10 年）和振幅（太阳黑子的数量）似乎在 1780 年至 1800 年之间发生变化。这产生了一些挑战。

3.2 计算 ACF

接下来我们要做的是确定 LSTM 模型是否是一个适用的好方法。LSTM 模型利用自相关性产生序列预测。我们的目标是使用批量预测（一种在整个预测区域内创建单一预测批次的技术，不同于在未来一个或多个步骤中迭代执行的单一预测）产生未来 10 年的预测。批量预测只有在自相关性持续 10 年以上时才有效。下面，我们来检查一下。

首先，我们需要回顾自相关函数（Autocorrelation Function，ACF），它表示时间序列与自身滞后项之间的相关性。stats 包库中的 acf() 函数以曲线的形式返回每个滞后阶数的 ACF 值。但是，我们希望将 ACF 值提取出来以便研究。为此，我们将创建一个自定义函数 tidy_acf()，以 tidy tibble 的形式返回 ACF 值。

tidy_acf <- function(data,
                     value,
                     lags = 0:20) {
    
    value_expr <- enquo(value)
    
    acf_values <- data %>%
        pull(value) %>%
        acf(lag.max = tail(lags, 1), plot = FALSE) %>%
        .$acf %>%
        .[,,1]
    
    ret <- tibble(acf = acf_values) %>%
        rowid_to_column(var = "lag") %>%
        mutate(lag = lag - 1) %>%
        filter(lag %in% lags)
    
    return(ret)
}

接下来，让我们测试一下这个函数以确保它按预期工作。该函数使用我们的 tidy 时间序列，提取数值列，并以 tibble 的形式返回 ACF 值以及对应的滞后阶数。我们有 601 个自相关系数（一个对应时间序列自身，剩下的对应 600 个滞后阶数）。一切看起来不错。

max_lag <- 12 * 50

sun_spots %>%
    tidy_acf(value, lags = 0:max_lag)

## # A tibble: 601 x 2
##      lag   acf
##    <dbl> <dbl>
##  1    0. 1.00 
##  2    1. 0.923
##  3    2. 0.893
##  4    3. 0.878
##  5    4. 0.867
##  6    5. 0.853
##  7    6. 0.840
##  8    7. 0.822
##  9    8. 0.809
## 10    9. 0.799
## # ... with 591 more rows

下面借助 ggplot2 包把 ACF 数据可视化，以便确定 10 年后是否存在高自相关滞后项。

sun_spots %>%
    tidy_acf(value, lags = 0:max_lag) %>%
    ggplot(aes(lag, acf)) +
    geom_segment(
        aes(xend = lag, yend = 0),
        color = palette_light()[[1]]) +
    geom_vline(
        xintercept = 120, size = 3,
        color = palette_light()[[2]]) +
    annotate(
        "text", label = "10 Year Mark",
        x = 130, y = 0.8,
        color = palette_light()[[2]],
        size = 6, hjust = 0) +
    theme_tq() +
    labs(title = "ACF: Sunspots")

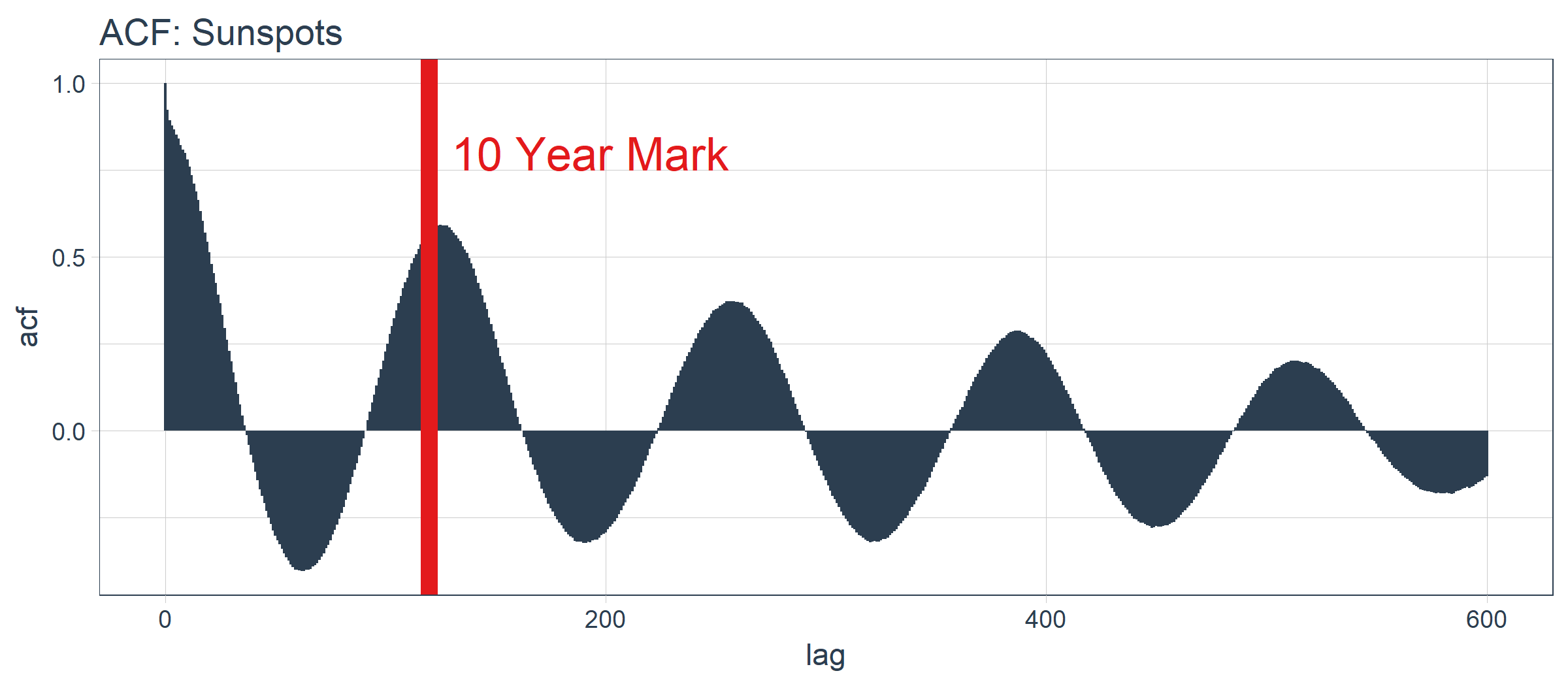
好消息。自相关系数在 120 阶（10年标志）之后依然超过 0.5。理论上，我们可以使用高自相关滞后项来开发 LSTM 模型。