说明：《数学分析原理》指 г.м.菲赫金哥尔茨 著《数学分析原理》（第一卷 第九版）高等教育出版社

 

---

 

整数和分数统称为有理数。有理数域不能完全满足数学定义的需求，比如人们无法将一个边长为1的正方形的对角线长度表示为有理数，也即 没有一个其平方能等于2的有理数 ${\frac{{p}}{{q}}}$（${p}$ 与 ${q}$ 是两个自然数）存在（需要说明的是原书中的自然数相当于我们说的正整数）。下面记录书中用反证法证明这一结论的过程。

 

证明 1

论点：没有一个其平方能等于2的有理数 ${\frac{{p}}{{q}}}$ （${p}$ 与 ${q}$ 是两个自然数）存在

证法：反证法

证明：假定有这样的分数 ${\frac{{p}}{{q}}}$ 存在，使得 ${{ \left( {\frac{{p}}{{q}}} \right) }\mathop{{}}\nolimits^{{2}}\text{?}=\text{?}2}$ 。可以假设这个分数是既约的，也就是说 ${p}$ 与 ${q}$ 无公因子，不可再约分。因 ${p\mathop{{}}\nolimits^{{2}}\text{?}=\text{?}2q\mathop{{}}\nolimits^{{2}}}$，所以 ${p}$ 是偶数。因 ${\frac{{p}}{{q}}}$ 既约，因而 ${q}$ 是奇数。设 ${p=2r}$（${r}$是整数），则有 ${p\mathop{{}}\nolimits^{{2}}\text{?}=\text{?}2q\mathop{{}}\nolimits^{{2}}\text{?}=\text{?}4r\mathop{{}}\nolimits^{{2}}}$，进而 ${q\mathop{{}}\nolimits^{{2}}\text{?}=\text{?}2r\mathop{{}}\nolimits^{{2}}}$ ，由此可推得 ${q}$ 是偶数，这与假设相矛盾，论点得证。

 

　　有理数域的不足在几何中简单地表现为 “不是所有的线段都能有长度”。例如，上述边长为1的正方形其对角线长度的平方为2，但其对角线长度自身不能用有理数表示，这可由论点1得出。

书中扩充有理数域、定义无理数是通过记录德国数学家戴德金关于讨论有理数域内分割的概念得出的。考虑把全部有理数的集合分成两个非空集合${A}$和${A'}$，即假定：

　　1. 每一个有理数在而且只在 ${A}$ 或 ${A'}$ 两个集合中的一个

　　2. 集合${A}$中的每一个数 ${a}$小于集合 ${A'}$ 中的每一个数 ${a'}$

满足这两个条件的对有理数域的分法称为“分割”。其中集合 ${A}$ 叫做分割的下类，集合A'叫做上类，分割可用 ${A|A'}$ 表示。书中证明，分割只能有以下三个类型：

1) 在下类 ${A}$ 中没有最大的数，而在上类 ${A}$ 中有最小的数 ${a}$；

2) 在下类 ${A'}$ 中有最大的数 ${r}$，而在上类 ${A}$ 中没有最小的数；

3) 既在下类中没有最大的数，又在上类中没有最小的数。

前两种分割是由有理数 ${r}$ 产生的（ ${r}$ 是 ${A}$ 与 ${A'}$ 两类中间的界数），或者说，这分割定义了有理数 ${r}$。第三种情形下的界数在有理数域不存在，分割不能定义任何有理数，故而引进了无理数，且规定 任何属于类型 3) 的分割定义了某一个无理数${α}$，${α}$就代替这缺少的界数。

下面用图示简单表示这三种情形，并证明第三种情形。

分割一：

 

 

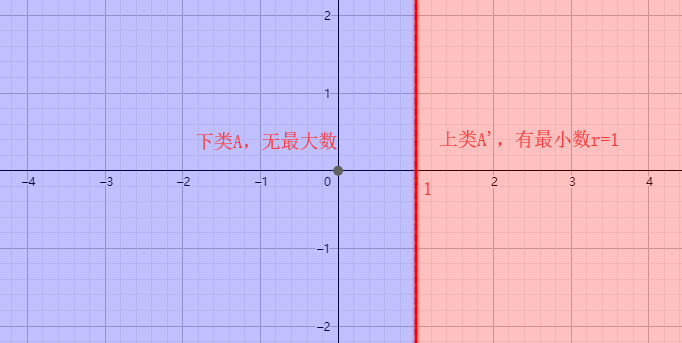
 分割二：

 

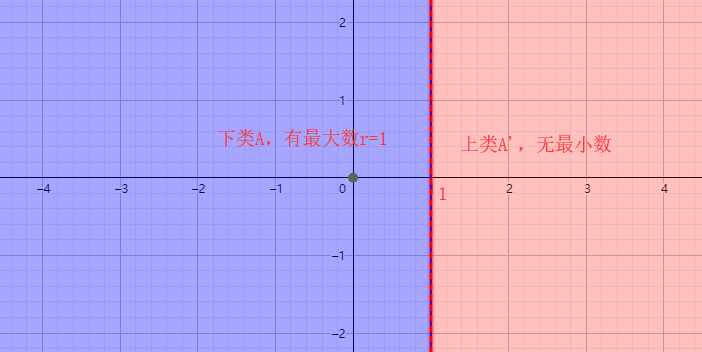
 分割三：

 

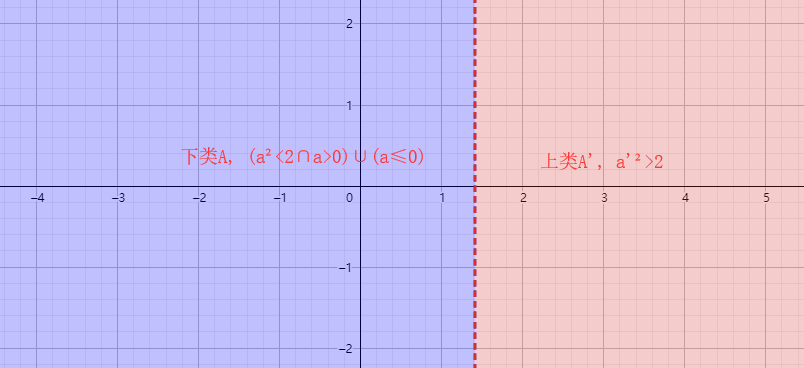
下面先记录书中对分割三第一种情形的证明，再仿照方法证明第二种情形。

 

证明 2

论点：在有理数域内，把一切使 ${a\mathop{{}}\nolimits^{{2}}\text{?} < \text{?}2}$ 的正有理数${a}$、${0}$及一切负有理数都归入${A}$类，把一切使 ${\mathop{{a'}}\nolimits^{{2}}\text{?} > \text{?}2}$ 的正有理数${a'}$ 归入${A'}$ 类，证明在 ${A}$ 类中既无最大数，在 ${A'}$ 类中也无最小数。

证法：放缩法不等式证明

证明：

　　(1). 首先，证明在 ${A}$ 类中无最大数

　　我们只需显示证明 ${a\mathop{{}}\nolimits^{{2}}\text{?} < \text{?}2}$ 的情况，${a\mathop{{}}\nolimits^{{2}}\text{?} \le \text{?}0}$ 的情况很明显成立。

　　设 ${a}$ 是 ${A}$ 类中的任一整数，则有${a\mathop{{}}\nolimits^{{2}} < 2}$，我们需证明如果可以有正数${n}$，使得

　　　　${{ \left( {a+\frac{{1}}{{n}}} \right) }\mathop{{}}\nolimits^{{2}}\text{?} < \text{?}2}$　　　　(1)，

也就是说让 ${a+\frac{{1}}{{n}}}$ 也属于${A}$类。展开不等式并移项可得

　　${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{?} < \text{?}2-a\mathop{{}}\nolimits^{{2}}}$　　　　(2)

又对于正数${n}$，不妨取 ${n > 1}$，则有 

${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{?} < \text{?}}\frac{{1}}{{n}}$

不等式两边同时加正数 ${\frac{{2a}}{{n}}}$ 可得

${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{?} < \text{?}\frac{{2a}}{{n}}+\frac{{1}}{{n}}}$

亦即 ${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{?} < \text{?}\frac{{2a\text{?}+1}}{{n}}}$

如果 ${n}$ 满足不等式 ${{\frac{{2a\text{?}+1}}{{n}}}\text{?} < \text{?}2-a\mathop{{}}\nolimits^{{2}}}$ ，则不等式成立 (2) 成立，进而不等式 (1) 成立。为此，只要取

　　${n\text{?} > \text{?}\frac{{2a+1}}{{2-a\mathop{{}}\nolimits^{{2}}}}}$

即可。由此可见，无论 ${a}$ 是 ${A}$ 类中怎样的一个正数，在 ${A}$ 类中总能找到大于 ${a}$ 的数。联系 ${a\mathop{{}}\nolimits^{{2}}\text{?} \le \text{?}0}$ 的情况，在 ${A}$ 类中无最大