CH 序列。建模者想知道在这种情况下她的估计值的行为。因此,GARCH 模型被认为是重要的。实际上,我刚刚描述的波动率聚集行为有时被描述为“GARCH行为”,因为它经常出现,GARCH 模型是解决它们的常用工具。(首字母缩略词 GARCH 代表广义自回归条件异方差性,它是对波动率时变性的统计学语言描述。)
\(\eta_t\) 可以是任何随机过程,但经常选择使用 i.i.d 的标准正态随机变量序列。这里 \(\eta_t\) 是模型中唯一的随机源。为了让 \(\text{GARCH}(1,1)\) 过程有一个稳定解,我们必须要求 \(\alpha + \beta > 0\)。在这种情况下,该过程具有 \(\frac{\omega} {1 - \alpha - \beta}\) 的长期方差。
估计 GARCH 参数
我上面写的过程是一个无限过程。索引 \(t\) 可以一直扩展到负数。显然在实践中我们没有观察到无限序列,因此如果我们想在实践中使用 \(\text{GARCH}(1,1)\) 模型,我们需要考虑类似的序列:
\[ \epsilon_t = \tilde{\sigma}_t \eta_t \]
\[ \tilde{\sigma}_t^2 = \omega + \alpha \epsilon_{t - 1}^2 + \beta \tilde{\sigma}_{t - 1}^2 \]
下面是新序列的独家秘方:
\[ \tilde{\sigma}_0^2 = \epsilon_0^2 = \frac{\omega}{1 - \alpha - \beta} \]
我们选择这个序列的初始值(前面描述的理论 \(\text{GARCH}(1,1)\) 序列没有初始值)!这个序列非常类似于理论序列,但它的整体上是可观察的,并且可以证明使用该序列估计的参数非常接近理论上无限 \(\text{GARCH}(1,1)\) 过程的参数。
当然,这些过程最重要的任务之一就是估算它们的参数。对于 \(\text{GARCH}(1,1)\) 过程,这些是 \(\omega\)、\(\alpha\) 和 \(\beta\)。一种基本方法是找到拟最大似然估计(QMLE)的估计量。假设我们有 \(t-1\) 时的观察值。在 QMLE 中,当假设 \(\eta_t\) 遵循标准正态分布(即 \(\eta_t \sim N(0,1)\))时,我们使用 \(\epsilon_t\) 的条件分布。我们假设一直到 \(t-1\),整个过程的历史记录已知,这意味着 \(\tilde{\sigma}_t\) 也是已知的(实际上我们需要知道的是 \(t-1\) 时间的值,但我离题了)。在这种情况下,我们有 \(\epsilon_t \sim N(0,\tilde{\sigma}_t^2)\)。设 \((x | \mathscr{f}_t) = f(x | \tilde{\sigma}_t^2)\) 是 \(\epsilon_t\) 的条件分布(所以 \(f(x | \tilde{\sigma}_t^2) = \frac{1}{\sqrt{2 \pi \tilde{\sigma}_t^2}} \exp \left(-\frac{x^2}{2 \tilde{\sigma}_t^2} \right)\))。然后是拟似然方程
\[ \mathscr{L}_T(\epsilon_1, ..., \epsilon_T) = \prod_{t = 1}^T f(\epsilon_t | \tilde{\sigma}_t^2) = (2 \pi)^{-n/2} \prod_{t = 1}^T \tilde{\sigma}_t^{-1} \exp\left(-\frac{1}{2}\sum_{t = 1}^T \frac{\epsilon_t^2}{\tilde{\sigma}_t^2} \right) \]
像大多数似然方法一样,统计学家不是直接优化拟似然函数,而是尝试优化对数似然函数,\(\log \left(\mathscr{L}_T(\epsilon_1,...,\epsilon_T)\right)\),经过一些工作后,不难发现这等同于最小化
\[ \sum_{t = 1}^T \left( \log(\tilde{\sigma}_t^2) + \frac{\epsilon_t^2}{\tilde{\sigma}_t^2} \right) \]
请注意,\(\omega\)、\(\alpha\) 和 \(\beta\) 通过 \(\tilde{\sigma}_t^2\) 包含在其中。对于最小化此数量的参数,没有闭式解。这意味着必须应用数值优化技术来找到参数。
可以证明,当以这种方式计算时,参数 \(\omega\)、\(\alpha\) 和 \(\beta\) 的估计量是一致的(意味着它们依概率收敛到它们的真实值),并且渐近地服从随高斯分布。这些属性我们可以与样本均值相联系,但是我们可能乐观地认为这些估计量的收敛速度与样本均值的收敛速度一样好,我们可以预期可比较的渐近行为。
理想情况下,参数应该像下面说明的过程一样。
library(ggplot2)
x <- rnorm(1000, sd = 1/3)
df <- t(
sapply(
50:1000,
function(t)
{
return(c("mean" = mean(x[1:t]), "mean.se" = sd(x[1:t])/sqrt(t)))
}))
df <- as.data.frame(df)
df$t <- 50:1000
ggplot(
df,
aes(x = t, y = mean)) +
geom_line() +
geom_ribbon(
aes(x = t, ymin = mean - 2 * mean.se, ymax = mean + 2 * mean.se),
color = "grey", alpha = 0.5) +
geom_hline(color = "blue", yintercept = 0) +
coord_cartesian(ylim = c(-0.5, 0.5))

fGarch 参数估计的行为
在继续之前,让我们生成 \(\text{GARCH}(1,1)\) 序列。在本文中,我使用了所有参数都等于 0.2 的过程。注意,对于 \(\text{GARCH}(1,1)\) 过程,长期方差将为 \(\frac{0.2}{1 - 0.2 - 0.2} = \frac{1}{3}\)。
set.seed(110117)
library(fGarch)
x <- garchSim(
garchSpec(
model = list(
"alpha" = 0.2, "beta" = 0.2, "omega" = 0.2)),
n.start = 1000,
n = 1000)
plot(x)
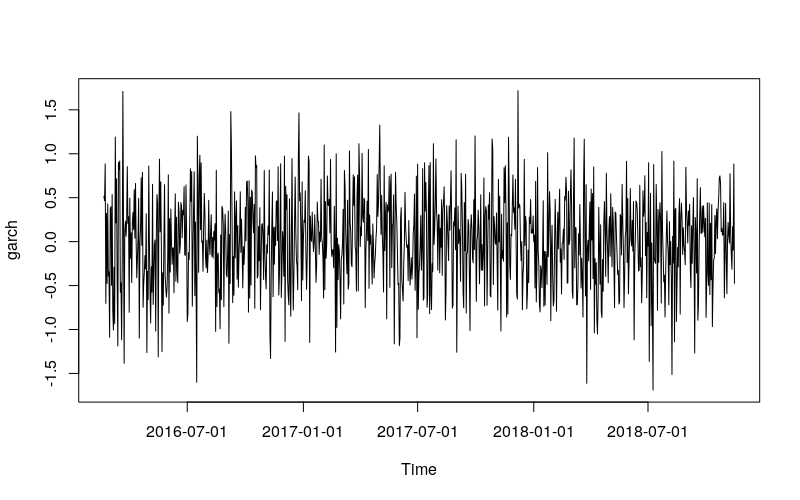
让我们看看 fGarch 的函数 garchFit() 所使用的参数。
args(garchFit)
## function (formula = ~garch(1, 1), data = dem2gbp, init.rec = c("mci",
## "uev"), delta = 2, skew = 1, shape = 4, cond.dist = c("norm",
## "snorm", "